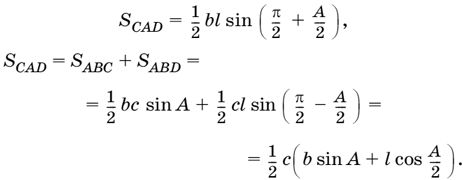![]()
Ответ.R /3
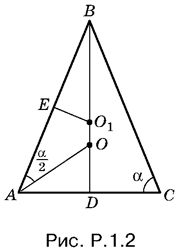
1.2. B треугольнике AOB (рис. P.1.2) известны: ∠ BAO = /2 , ∠ AOB = /2 + /2, BO = m· По теореме синусов находим AB = m ctg /2· Теперь можно найти AC и R = ВО1:
AC = 2AD = 2АВ sin (/2 − α) = 2АВ cos α = 2m ctg /2 cos α,
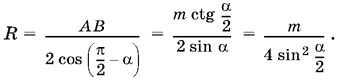
Ответ. 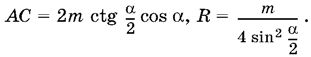
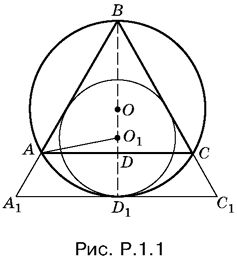
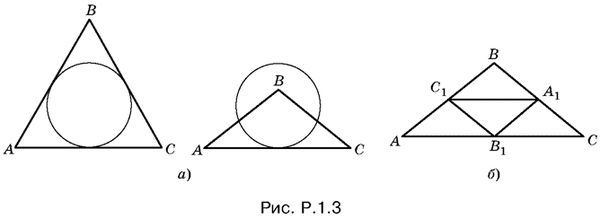
1.3. Условие задачи может быть геометрически осуществлено в двух случаях (рис. Р.1.3, а), т. е. когда треугольник либо правильный, либо равнобедренный тупоугольный (докажите). Решить эту задачу можно сразу для обоих случаев. На рис. Р.1.3, б изображены треугольник ABC и треугольник А1В1С1, составленные из средних линий первого треугольника. Треугольник А1В1С1 подобен треугольнику ABC с коэффициентом подобия половина. Следовательно, радиусы окружностей, описанных около этих треугольников, относятся как один к двум.
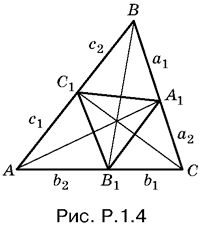
1.4. Если сторона а треугольника ABC биссектрисой АА1 разделена на отрезки а1 и а2, то можно записать следующие соотношения (рис Р. 1.4.):
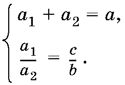
Решая эту систему уравнений относительно a1 и а2, получим
![]()
Вычислим аналогично отрезки, на которые разделены стороны b и с треугольника ABC:
![]()
Так как отношение площадей треугольников, имеющих общий угол, равно отношению произведений сторон, между которыми лежит этот общий угол, то
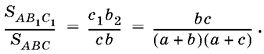
Аналогично находим
![]()
Теперь найдем отношение 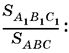
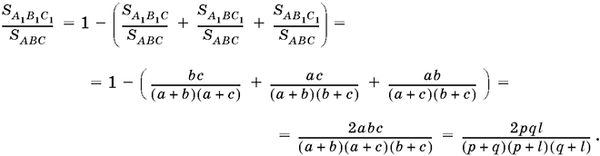
Ответ.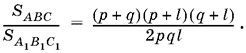
1.5. Выразим площадь треугольника ABC через радиус r вписанной окружности и углы А, B и С треугольника. Вначале запишем
SABC = SAOB + SBOC + SCOA
(рис. P.1.5).
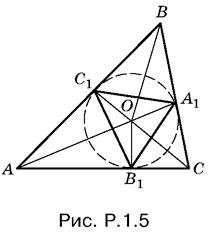
Так как
SAOB = ½АО · ВО sin OB,
где 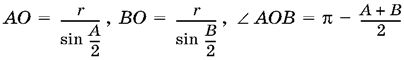
и, следовательно, sin ∠AOB = sin /2 = cos /2 , то
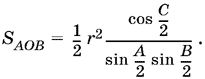
Аналогично находим SBOC и SCOA и вычисляем искомую площадь:
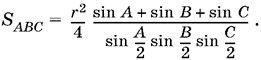
Выразим теперь через r, А, B и С площадь треугольника А1В1С1. Разобьем и его на три треугольника:
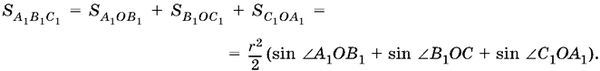
Чтобы найти угол А1ОВ1, рассмотрим четырехугольник А1ОВ1С. B этом четырехугольнике два угла прямых, а потому два других - угол А1ОВ1 и угол С - образуют в сумме развернутый угол, т. е. угол А1ОВ1 равен π − С. Аналогично находим углы В1ОС1 и С1ОА1.
Итак,
![]()
Остается найти отношение ![]()
Ответ. 2 sin /2 sin /2 sin /2 .
1.6. Так как B = 3С, то из соотношения между площадями мы получим
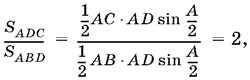
т. е. /AB = 2, откуда, в силу теоремы синусов, /sin C = 2. Вспоминая, что по условию B = 3С, придем к тригонометрическому уравнению sin 3С = 2 sin С. Домножим обе части уравнения на cos С, получим sin 3С cos 3С = sin 2С. Преобразовав левую часть в сумму синусов, придем к уравнению
sin 4С + sin 2С = 2 sin 2С, или sin 4С = sin 2С.
Так как C - угол треугольника, меньший 1 (ведь 3C и C - углы одного треугольника), то последнее уравнение может выполняться только в том случае, если
4C = π − 2C, т. е. C = /6 .
Находим остальные углы:
B = 3С = /2, A = /3.
Ответ./3, /6, /2.
1.7. С одной стороны, площадь треугольника CAD (рис. Р.1.7) можно выразить через стороны b, l и угол между ними, а с другой стороны, - как сумму площадей треугольников АВС и ABD: