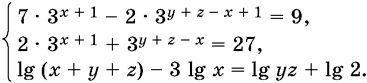Глава 11
Логарифмические и показательные уравнения и системы
Если а, где а и p - действительные числа, существует, то
|a| = |а| (1)
По определению logа N есть число, удовлетворяющее равенству
где а > 0 и а ≠ 1.
Формулы
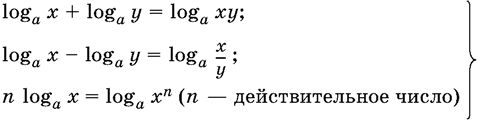
(2)
называются формулами потенцирования. Первые две являются неабсолютными тождествами (см. введение к главе 9); при четных n и третья формула оказывается неабсолютным тождеством. Применение этих формул при решении уравнений (под применением формулы мы понимаем замену в уравнении выражения, стоящего в ее левой части, на выражение, стоящее справа) может привести только к приобретению посторонних решений.
Формулы (2), прочитанные справа налево, называются формулами логарифмирования. Чтобы формулы логарифмирования не приводили к потере решений, ими пользуются в виде
logахy = logа |x| + logа |y|;
logа/y = logа |x| − logа |y|;
logаx = 2k logа |x| (k - целое, k ≠ 0).
Следующие формулы позволяют переходить от логарифма с одним основанием к логарифму с другим основанием:
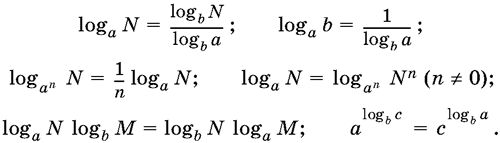
Если в третьей из этих формул n = 2k, то в правой части нужно писать вместо основания а основание |а|.
Формула
(3)
является неабсолютным тождеством, так как ее правая часть перестает существовать при f(x) = 1, в то время как левая часть при соответствующих значениях x может существовать и обращаться в нуль.
Таким образом, применение формулы (3) может привести к потере решений, при которых f(x) = 1.
При решении уравнений вида
φ(x) = φ(x) (4)
нужно воспользоваться условием равенства показателей: если φ(x) ≠ −1, 0, +1, то следствием уравнения (4) является уравнение
f(x) = g(x). (5)
Пусть x = а - корень уравнения (4). Тогда
φ(а) = φ(а).
В силу (1) можно записать, что
|φ(а)| = |φ(а)|.
Так как |φ(x)| ≠ 0, 1 и |φ(x)| > 0, то по свойству показательной функции имеем
f(а) = g(а),
т. е. x = а - корень уравнения (5).
Случаи, когда φ(x) равно −1, 0 или 1, нужно рассмотреть отдельно.
Решая уравнение (4), следует иметь в виду, что выражения вида /0 и 0 не имеют смысла.
11.1. Найдите log5 6, если lg 2 = а, lg 3 = b.
11.2. Найдите lg 122,5, если lg 5 = а, lg 7 = b.
11.3. Решите уравнение
11.4. Для каждого действительного числа а решите уравнение
9 − 4 · 3 − a = 0.
11.5. Для каждого действительного числа а решите уравнение
144 − 2 · 12 + а = 0.
Решите уравнения:
11.6. 
11.7.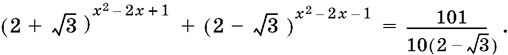
11.8. 
11.9.
11.10. log3(3 − 1) log3 (3 − 3) = 6.
11.11.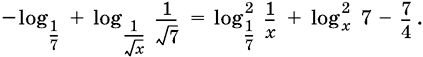 
11.12. 
11.13. 
11.14. 
11.15. log0,5xx² − 14 log16xx³ + 40 log4x√x = 0.
11.16.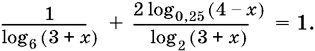 
11.17. 
11.18. 
11.19.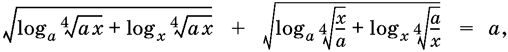 
где а > 0, а ≠ 1.
11.20. Найдите неотрицательные решения системы уравнений
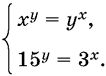
Решите системы уравнений:
11.21.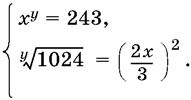 
11.22.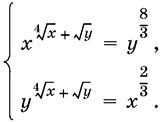 
11.23.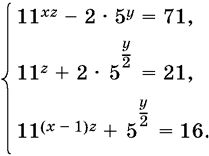 
11.24.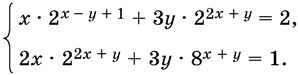 
11.25.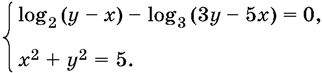 
11.26.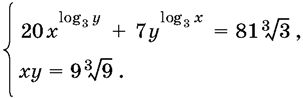 
11.27.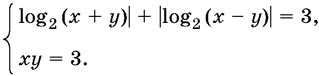 
11.28.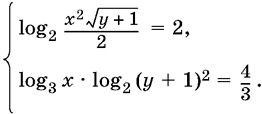 
11.29.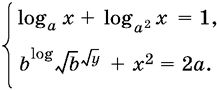 
11.30. 