![]()
10.8. Докажите, что ![]() при n > 1.
при n > 1.
10.9. Докажите неравенство
/b + /c + /a > 3
где а, b и с - положительные и не равные друг другу числа, не пользуясь неравенствами между средним арифметическим и средним геометрическим трех чисел.
10.10. Докажите, что
а² + b² + с² ≥ 4S√3,
где а, b, с - стороны, а S - площадь некоторого треугольника.
10.11. Докажите, что
(x − 1)(x − 3)(x − 4)(x − 6) + 10 ≥ 1
при всех действительных значениях x.
10.12. Докажите, что если действительные числа x, у, z, не равные нулю, удовлетворяют равенствам:
x + у + z = xуz и x² = уz,
то
x² ≥ 3.
10.13. Докажите, что если x, у, z - действительные числа, удовлетворяющие равенствам
x + у + z = 5, уz + zx + xу = 8,
то
1 ≤ x ≤ /3, 1 ≤ y ≤ /3, 1 ≤ x ≤ /3.
10.14. Решите неравенство
аx² + x + 1 > 0,
где а ≠ 0 - произвольное действительное число.
10.15. Найдите все действительные значения m, при которых квадратный трехчлен x² + mx + (m² + 6m) будет отрицателен при всех значениях x, удовлетворяющих неравенству 1 < x < 2.
10.16. Найдите все действительные значения а, при которых корни многочлена x² + x + а будут действительными и оба корня будут больше а.
10.17. При каких значениях к корни многочлена
k²x² + kx − 2
будут действительными и один корень по абсолютной величине будет больше 1, а другой по абсолютной величине будет меньше 1?
10.18. Найдите все действительные значения m, для которых неравенство
тx² − 4x + 3m + 1 > 0
удовлетворяется при всех положительных значениях x.
Решите неравенства:
10.19. |x² − 2x − 3| < 3x − 3.
10.20. |x − 3| > |x + 2|.
10.21. ![]()
10.22. ![]()
10.23. ![]()
10.24. ![]()
10.25. ![]()
10.26. ![]()
10.27. 4 ≤ 3 · 2 + x + 4.
10.28. 4x² + 3 + x · 3 < 2x² · 3 + 2x + 6.
10.29. ![]()
Решите неравенства:
10.30. (4x² + 12x + 10) ≥ (4x² + 12x + 10).
10.31.x > а²x.
10.32. ![]()
10.33. ![]()
10.34. ![]()
10.35. 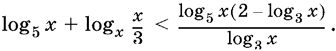
10.36. log2 (2 − 1) log½ (2 − 2) > −2.
10.37. log|x + 6| 2 · log2(x² − x − 2) ≥ 1.
10.38. 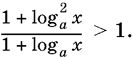
10.39. logkxx + logx(kx²) > 0, где 0 < k < 1.
10.40. logx[log2(4 − 6)] ≤ 1.
10.41. ![]()
10.42.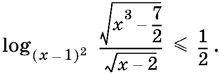
10.43. |√2 |x| − 1| · 1ох2 (2 − 2x²) > 1.
10.44. 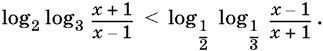
10.45. logx² − 1 (3x − 1) < logx² − 1x².
10.46.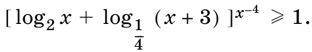
10.47. При каких значениях у верно следующее утверждение: "Существует хотя бы одно значение x, при котором удовлетворяется неравенство
2 log0,5y² − 3 + 2x log0,5y² − x² > 0"?
10.48. При каких значениях а из неравенства
x² − а(1 + а²)x + а < 0
следует неравенство
x² + 4x + 3 < 0?
10.49. Для каждого действительного а решите неравенство
![]()
10.50. Решите неравенство
(x² + 8x + 15)2 > x² + 7x + 10.
10.51. Определите, какие из чисел −4, −1, 1, 4 являются решениями неравенства
|0,5 − lg 5|x ≤ 0,5 − lg 5.
10.52. Решите неравенство
(√5 − 2) ≤ (√5 + 2).
10.53. Решите неравенство
![]()