откуда
Обратите внимание, что следующее "доказательство" неравенства является логически некорректным.
Если 
и, следовательно,
что очевидно.
Некорректность приведенных рассуждений состоит в том, что в качестве исходного пункта взято доказываемое неравенство. Таким образом установлено, что если 
то (√а − √b)² ≥ 0. Однако верное следствие может быть получено из ложной посылки. Если те же рассуждения провести в обратном порядке, то мы получим корректное доказательство, аналогичное тому, которое приведено выше под номером 3).
Решение неравенств. Система, совокупность. Решить неравенство - значит, найти все системы значений входящих в него неизвестных, при которых неравенство истинно, или доказать, что таких систем значений нет.
Если два или несколько неравенств должны удовлетворяться одновременно, то говорят, что они образуют систему.
Если достаточно, чтобы удовлетворялось одно из двух или нескольких неравенств, то говорят, что эти неравенства образуют совокупность.
Неравенства, образующие систему, записывают одно под другим, а сбоку ставят фигурную скобку - знак системы.
Например,
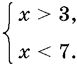
Решение этой системы показано на рис. 10.1 двойной штриховкой. Эта же система неравенств может быть записана так: 3 < x < 7.
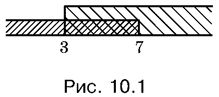
Совокупность неравенств записывают либо в строку, либо в столбец и ставят слева квадратную скобку. Это позволяет не путать совокупность неравенств с системой. Запись
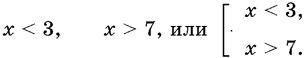
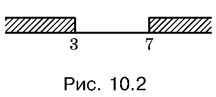
означает, что число x должно лежать на любом из заштрихованных на рис. 10.2 интервалов.
Решить систему, состоящую из нескольких совокупностей неравенств, - значит, найти все значения неизвестного, удовлетворяющие всем входящим в систему совокупностям.
Пример 1. Решить систему совокупностей неравенств
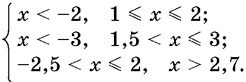
Решение первой совокупности изображено на рис. 10.3 с помощью двух прямоугольников (левая сторона одного из них бесконечно отодвинута влево), расположенных над точками, удовлетворяющими этой совокупности. Аналогично на этом же рисунке изображены решения второй и третьей совокупностей.
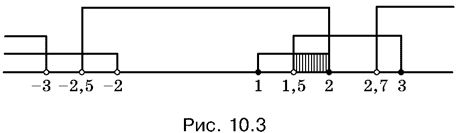
Чтобы избежать путаницы, мы для разных совокупностей строим прямоугольники различной высоты. Особо внимательно нужно следить за концами интервалов: если неравенство строгое, то будем рисовать в конце интервала светлый кружок, а если нестрогое, то - черный кружок. Специально разберите случаи, когда одна и та же точка оказывается и светлой, и темной - для системы и совокупности неравенств.
Точки числовой оси, над которыми расположены три прямоугольника разной высоты (см. рис. 10.3), дают решение системы: 1,5 < x ≤ 2.
Упражнения
1. Что произойдет с совокупностью неравенств, если к ней добавить неравенство, не имеющее решений?
2. Что произойдет с системой неравенств, если к ней добавить неравенство, не имеющее решений?
3. Решите систему двух совокупностей неравенств
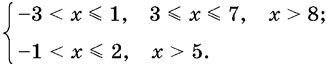
Метод интервалов. Рассмотрим неравенства типа
(1)
Начнем предварительно с неравенства (x − 2)(x − 3) > 0. Его нередко решают следующим образом. Произведение двух множителей положительно тогда и только тогда, когда оба множителя одного знака, т. е. данное неравенство равносильно совокупности двух систем
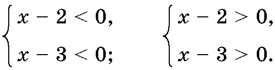
Чтобы убедиться в нерациональности такого способа решения, достаточно применить его к решению неравенства, левая часть которого содержит, например, десять множителей
(x − 1)(x − 2)...(x − 10) > 0. (2)
Несложный подсчет показывает, что в этом случае пришлось бы рассматривать совокупность, состоящую из 512 систем по 10 неравенств в каждой системе.
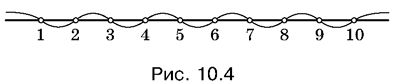
Решим неравенство (2) с помощью более рационального приема, называемого методом интервалов. Отметим на числовой оси все корни многочлена, стоящего в левой части неравенства (рис. 10.4). Когда x расположен правее самого большого корня (x > 10), многочлен будет положительным, так как каждый множитель положителен. Если двигаться по оси в отрицательном направлении, то при переходе через точку x = 10 множитель x − 10 поменяет знак. В произведении появится один отрицательный множитель, а девять останутся положительными, в результате чего многочлен поменяет знак, так как появится дополнительный отрицательный множитель. Далее перемена знака произведения произойдет при переходе через каждую из обозначенных на рис. 10.4 точек. (Области, где многочлен положителен, отмечены на рис. 10.4 дугой сверху, а области, где он отрицателен, - дугой снизу.) Теперь легко записать решение неравенства (2):
x < 1, 2 < x < 3, 4 < x < 5, 6 < x < 7, 8 < x < 9, x > 10.
Приемы, позволяющие решать более сложные неравенства типа (1), станут понятны, если вы разберете примеры 2 и 3 и следующие за ними упражнения.
Пример 2. Решить неравенство (x + 3)(2x + 2)(x − 4)²(5 − x) > 0.
Перепишем неравенство в виде
(x + 3)(x + 1)(x − 4)²(x − 5) < 0,
где в каждой скобке стоит двучлен с коэффициентом 1 при x. Множитель (x − 4)² всегда неотрицателен и только в точке x = 4 обращается в нуль. Поэтому его влияние на решение неравенства
ограничивается тем, что он исключает точку x = 4 (рис. 10.5). Остается проследить чередование знаков в неравенстве
(x + 3)(x + 1)(x − 5) < 0.
Ответ. x < −3, −1 < x < 4, 4 < x < 5.
Пример 3. Решить неравенство
(3)
Данное неравенство не удовлетворяется в тех точках, где множители, стоящие в знаменателе, обращаются в нуль (x = 4, x = 2). Поэтому исключим эти точки из дальнейшего рассмотрения, обозначив их на рис. 10.6 светлыми кружками.
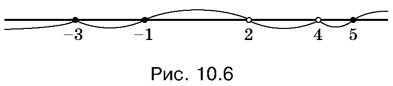
В точках же, в которых обращается в нуль числитель (x = −3, x = −1, x = 5), неравенство превращается в равенство, т. е. эти точки должны войти в решение неравенства (3). Отметим их на рисунке черными кружками).
Множители (x + 3)² и (x − 4)², не меняющие знака на всей числовой оси, можно опустить, так как их влияние уже учтено. Во всех остальных точках неравенство (3) равносильно такому:
(x + 1)(x − 5)(x − 2) < 0.
Ответ. x ≤ −1, 2 < x < 4, 4 < x ≤ 5.