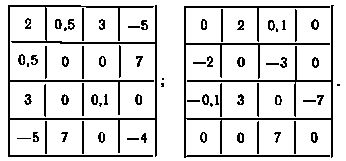
Ясно, что не все элементы таких матриц могут быть выбраны произвольно. Можно убедиться, что из n элементов для симметричной матрицы независимыми могут быть только 1/2 n (n + 1), а для кососимметричной -1/2 n (n + 1) элементов.
- 35 -
Комплексно-сопряженная и транспонированная матрица (A) называется сопряженной с А и обозначается A*. Матрица, равная своей сопряженной, т.е. A = (A̅) = A*, называется эрмитовой. Если A = -(A̅), то А - косоэрмитова матрица.
Легко показать, что транспонирование произведения АВ равно произведению транспонированных матриц, взятых в обратном порядке: (AB) = BA. Дважды транспонированная матрица равна исходной, т.е. (A) = A.
7. Матричная запись системы линейных уравнений. Первоначально матрицы были введены для упрощения записи систем линейных уравнений, что и обусловило и определение основных матричных операций. Система линейных уравнений:
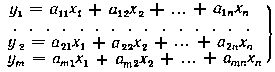
записывается одним матричным равенством
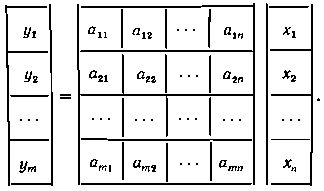
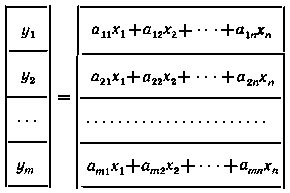
Действительно, перемножив в правой части равенства ( m × n ) - матрицу на столбцевую матрицу, получим
- 36 -
Из равенства матриц-столбцов следуют равенства для соответствующих элементов, которые совпадают с исходной системой уравнений. Если обозначить
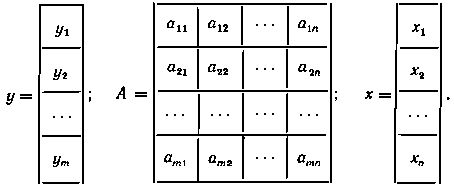
то матричное равенство запишется еще короче
y = Ax.
Такое представление системы линейных уравнений оказалось возможным благодаря правилу умножения матиц, которое наилучшим образом подходит для этой цели. Однако исторически дело обстояло как раз наоборот: правила действий над матрицами определялись, прежде всего, исходя из удобства представлений систем линейных уравнений.
8. Линейные преобразования. Систему уравнений, записанную в начале предыдущего пункта, можно рассматривать как линейное преобразование совокупности величин x1, x2, ..., xn в совокупность y1, y2, ..., ym. Это преобразование полностью определяется коэффициентами aij (i = 1, 2, ..., m; j = 1, 2, ..., n). На языке матриц линейное преобразование y = Ax означает преобразование столбца х в столбец у, которое определяется матрицей преобразования А.
Пусть величины x1, x2, ..., xn получаются из некоторой совокупности величин z1, z2, ..., zn посредством линейного преобразования x = Bz, где x и z - столбцы соответствующих величин; В - матрица их преобразования. Тогда формальной подстановкой х в первое матричное уравнение получаем
y = Ax = A(Bz) = (AB)z = Cz,
где C = AB - матрица преобразования величин z и y. К этому же результату можно прийти путем подстановки значений x1, x2, ..., xn из второй системы уравнений в первую с учетом введенного ранее правила умножения прямоугольных матиц.
9. Обратная матрица. В обычной алгебре два числа, произведение которых равно единице, называют взаимно обратными. Число, обратное числу a обозначают через a и по определению aa = 1
- 37 -
Аналогично в матричной алгебре две квадратные матрицы, произведение которых равно единичной матрице, т.е. AA = AA = 1, называют взаимно обратными ( A обратна A). Однако дальше этого аналогия не проходит.
Выражение ab, где a и b - числа, можно представить как частное от деления b на a, но для матриц такое представление не имеет смысла и в общем случае AB ≠ BA. Поэтому вместо операции деления В на А различают левое частное AB и правое частное BA, которые сводятся к умножению слева или справа на обратную матрицу A.
Способ обращения матрицы проще всего установить, рассматривая решение системы n линейных уравнений с n неизвестными:
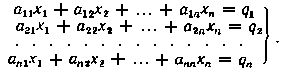
В матричной форме эта система уравнений запишется как Ax = q, где А - квадратная матрица n-го порядка, называемая матрицей системы: x и q - столбцевые матрицы неизвестных переменных и свободных членов:
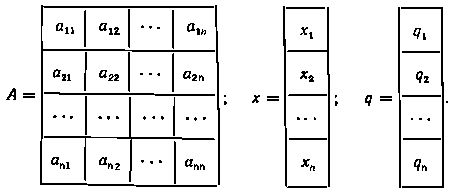
Матричное уравнение Ax = q решается умножением обеих его частей слева на обратную матрицу A т.е. AAx = Aq в результате получаем x = Aq.
В соответствии с правилом Крамера неизвестные xk(k = 1, 2, ..., n) определяются соотношением:
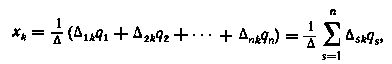
где Δ - определитель системы уравнений Δsk - алгебраические дополнения.
- 38 -
Определитель Δ представляет собой числовую функцию, которая вычисляется по определенным правилам на основании квадратной таблицы, состоящей из коэффициентов системы уравнений

Табличное представление определителя Δ по форме совпадает с матрицей системы уравнений, т.е. состоит из тех же элементов и в том же порядке, что и матрица А. В таких случаях его называют определителем матрицы А и записывают Δ = detA.
Алгебраическое дополнение Δsk вычисляется как определитель матрицы, полученной удалением из матицы A s-й строки и k-го столбца, причем этот определитель умножается еще на (-1). Величину Δsk называют также алгебраическим дополнением элемента ask матрицы A. Часто определитель матрицы А обозначается через |A|, а алгебраическое дополнение - через Ask.
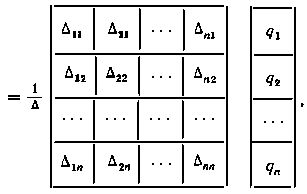
Записав для всех элементов столбцевой матрицы x выражения по правилам Крамера, получим решение системы уравнений в виде:

- 39 -
откуда, сравнивая с Aq, имеем
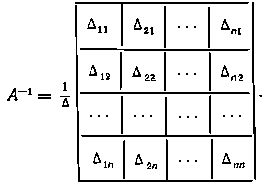
Из полученного выражения следует правило определения обратной матрицы: 1) элементы aij данной матрицы A n-го порядка заменяются их алгебраическими дополнениями Δij: 2) матрица алгебраических дополнений транспонируется, в результате чего получаем присоединенную или взаимную матрицу к А ( она обозначается через AdjA); 3) вычисляется определитель Δ матрицы А и присоединенная матрица AdjA умножается на величину, обратную этому определителю.
Обратная матрица существует для матрицы А при условии, что detA ≠ 0. Такие матрицы называются неособенными, в отличие от особенных (вырожденных), определитель которых равен нулю. Ниже вычисление обратной матрицы иллюстрируется примером: