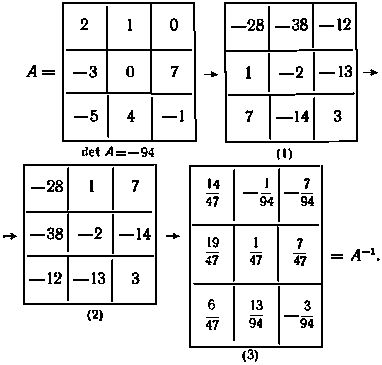
- 40 -
Матрица, обратная произведению двух матриц, равна переставленному произведению матриц, обратных исходным, т.е. (AB) = BA. Действительно, умножив обе части этого равенства на АВ, приходим тождеству E = BA(AB), так как B(AA)B = BEB = BB =E, где E - единичная матрица n-го порядка.
10. Блочные матрицы. Часто матрицу удобно разбить вертикальными и горизонтальными линиями на блоки которые являются матрицами меньших размеров и при выполнении операций рассматриваются как элементы исходных матриц. Операции над блочными матрицами выполняются по сформулированным выше правилам при условии, что эти операции допускаются размерами соответствующих матриц.
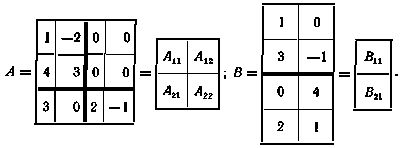
Пусть, например, матрицы А и В разбиты на блоки (жирными линиями) так, чтобы для соответствующих блоков имела смысл операция умножения, т.е.
По правилу умножения прямоугольных матриц можно записать:
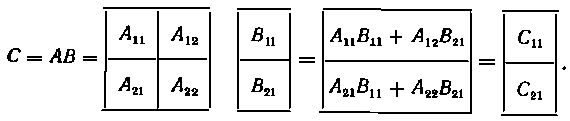
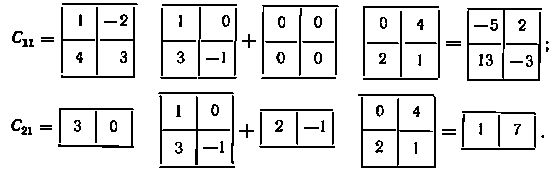
Вычислим блоки C11 и C21 матрицы C:
- 41 -
В результате имеем
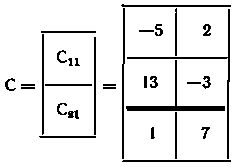
Конечно, тот же результат получается и при непосредственном перемножении матриц. Но разбиение на блоки позволяет оперировать с матрицами меньших размеров ( это бывает необходимо, например, когда не хватает места на бумаге или ячеек оперативной памяти машины) и особенно удобно, если можно выделить нулевые блоки.
Задачи и упражнения.
1. Любая матрица является прямоугольной таблицей. Справедливо ли обратное утверждение, т.е. можно ли считать всякую прямоугольную таблицу матрицей? Если нет,то какие дополнительные требования выдвигаются с позиций матричной алгебры?
2. Какие из приведенных ниже совокупностей объектов представляют собой матрицы:
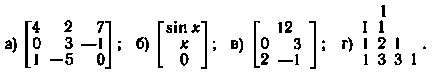
3. Укажите, какие из приведенных ниже матриц являются равными между собой (при x=2)%
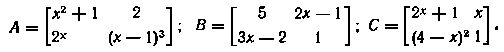
4. При каком значении x матрицы А и В равны:
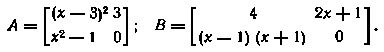
5. Найти сумму А + В и разность А - В матриц:
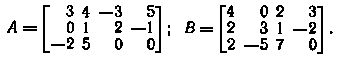
6. Найти произведения АВ и ВА и сравнить полученные результаты для матриц:
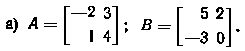
- 42 -
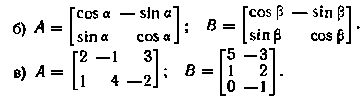
7. Проверить дистрибутивность умножения слева А(В + С) = АВ + АС и справа (А + В)С = АС + ВС относительно сложения для следующих матриц:
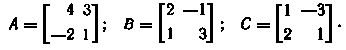
8. Найти все матрицы, перестановочные с матрицей
![]()
9. Каким условиям в общем случае должны удовлетворять элементы квадратных матиц А и В второго порядка, чтобы они были перестановочными (АВ = ВА)? Как выглядят эти условия для случая, когда А симметричная матрица?
10. При каких условиях справедливы матричные соотношения:
(A + B) = A + 2AB +B; (A-B)(A+B) = A - B?
11. Каким условиям должны удовлетворять элементы ненулевых квадратных матриц А и В, чтобы АВ = 0?
12. К каким типам относятся матрицы:
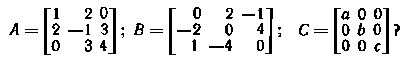
13. Построить транспонированную A, комплексно-сопряженную A̅ и сопряженную А* для матрицы
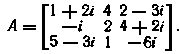
14. Показать, что матрица
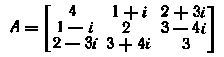
является эрмитовой. Что можно сказать о диагональных элементах любой эрмитовой матрицы?
15. Какого типа должна быть квадратная матрица А, чтобы она была перестановочной с диагональной матрицей D того же порядка, т.е. чтобы AD = DA?
16. К какому типу относятся треугольные матрицы, если они кроме того: а) симметричные, б) кососимметричные?
17. Показать, что (A̅B̅) = A̅ B̅ и (AB)* = B* A*.
18. Проверить соотношение (AB)* = B*A* для матриц задачи 6в.
19. Показать, что произведение AA существует для любой матрицы А и является симметричной матрицей.
- 43 -
20. Для заданных матриц найти обратные и проверить соотношение AA = 1:
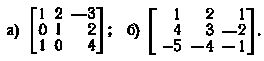
21. Найти матрицы, обратные заданным, и проверить соотношение (AB) = BA:
![]()
22. Дана система уравнений:
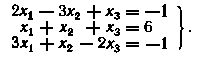
Записать эту систему в матричной форме Ax = q, вычислить обратную матрицу А и записать решение системы.
23. Зависимости между токами и напряжениями четырехполюсника (рис. 6, а) можно представить одной из систем уравнений:
![]()
Рис. 6. Соединение четырехполюсника: а - четырехполюсник; б - последовательное соединение; в - параллельное соединение.
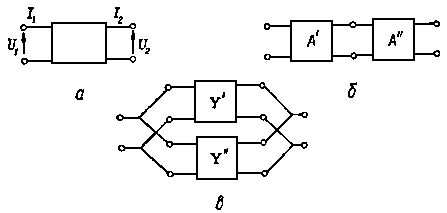
а) Записать эти уравнения в матричной форме и установить зависимости между элементами матриц:
![]()
б) Показать, что матрица А последовательного соединения четырехполюсников (рис 6. б) равна произведению их матриц A' и A'', т.е. A = A' A'' (в порядке следования).
в) Показать, что матрица Y параллельного соединения четырехполюсников (рис. 6, в) равна сумме их матриц Y' и Y'', т.е. Y = Y' + Y''.
- 44 -
24. Выполнить умножение матриц, воспользовавшись разбиением их на блоки:
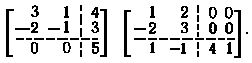
Проверить результат непосредственным умножением матриц.
4. Графы
1. Происхождение графов. Многие задачи сводятся к рассмотрению совокупности объектов, существенные свойства которых описываются связями между ними. Например, глядя на карту автомобильных дорог, можно интересоваться только тем, имеется ли связь между некоторыми населенными пунктами, отвлекаясь от конфигурации и качества дорог, расстояний и других подробностей. При изучении электрических цепей на первый план может выступать характер соединений различных ее компонентов - резисторов, конденсаторов, источников и т. п. Органические молекулы образуют структуры, характерными свойствами которых являются связи между атомами. Интерес могут представлять различные связи и отношения между людьми, событиями, состояниями и вообще между любыми объектами.
В подобных случаях удобно рассматриваемые объекты изображать точками, называемыми вершинами, а связи между ними - линиями (произвольной конфигурации), называемыми ребрами. Множество вершин V, связи между которыми определены множеством ребер Е, называют графом и обозначают 0 = (V, Е).
Первая работа по графам была опубликована двадцатилетним Леонардом Эйлером в 1736 г., когда он работал в Российской Академии наук. Она содержала решение задачи о кенигсбергских мостах