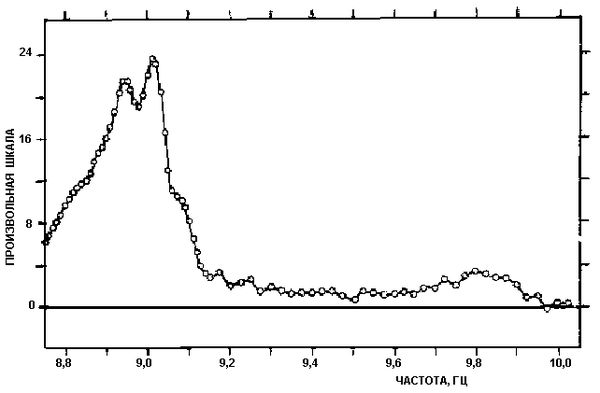
Рис. 11. Спектр
Рассматривая кривую, мы обнаруживаем замечательное падение мощности в окрестности частоты 9,05 гц. Точка, в которой спектр по существу исчезает, выражена весьма отчетливо и дает объективную величину, которая может быть проверена с гораздо большей точностью, чем любая величина, встречавшаяся до сих пор в электроэнцефалографии. Существуют указания, что на других кривых, которые мы получили, но которые несколько сомнительны в своих подробностях, за этим внезапным падением мощности довольно скоро следует крутой подъем. Таким образом, кривая имеет здесь как бы впадину. Но даже если догадка не верна, многое говорит за то, что концентрация мощности в пике соответствует отсасыванию мощности из области, где кривая идет низко. Стоит отметить, что в полученном спектре основная часть пика лежит в диапазоне шириной 1/3 гц. Любопытно, что на другой электроэнцефалограмме того же субъекта, записанной через четыре дня, ширина пика почти не изменилась и, насколько можно судить, форма его также сохранилась в [c.279] какой-то мере. Есть основание полагать, что у других субъектов ширина пика будет другой и даже меньшей. Для вполне удовлетворительной проверки этого необходимы дальнейшие изыскания.
Весьма желательно, чтобы исследования, здесь упомянутые, были продолжены более точными инструментальными работами, с лучшими приборами, и чтобы благодаря этому гипотезы, высказанные здесь, могли быть окончательно подтверждены или окончательно опровергнуты.
Теперь я хочу перейти к вопросу выборки. Для этого мне понадобятся некоторые идеи из моих предыдущих работ об интегрировании в пространстве функций. С помощью этого аппарата мы сможет построить статистическую модель непрерывного процесса с заданным спектром. Хотя такая модель не воспроизводит в точности процесса формирования мозговых волн, она достаточно близка к нему, чтобы доставить статистически значимую информацию о том, какой среднеквадратической ошибки можно ожидать в спектрах волн, подобных представленному выше.
Здесь я сформулирую без доказательств ряд свойств некоторой действительной функции х(t, α), уже излагавшихся в моей статье по обобщенному гармоническому анализу и в других работах. Действительная функция х(t, α) зависит от переменной t, изменяющейся от -∞ до ∞, и от переменной α, изменяющейся от 0 до 1. Она изображает одну пространственную координату броунова движения, зависящую от времени t и параметра α статистического распределения. Выражение
(10.09)
определяется для всех функций φ(t) класса Лебега L, [c.280] в интервале от -∞ до +∞. Если φ(t) имеет производную, принадлежащую L, то выражение (10.09) понимается как
(10.10)
и затем определяется для всех функций φ(t) из L некоторым вполне определенным предельным процессом. Другие интегралы
(10.11)
вводятся аналогичным образом.
Основная теорема, используемая нами, утверждает, что
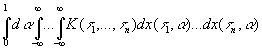(10.12)
можно найти, положив
, (10.13)
где переменные τk образуются всеми возможными способами путем отождествления всех пар переменных σk, друг с другом (если n четно), и образовав
(10.14)
Если n нечетно, то
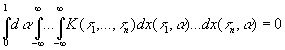(10.15)
Другая важная теорема, касающаяся этих стохастических интегралов, гласит: пусть F{g} - функционал [c.281] от g(t), такой, что F[x(t, α)] есть функция, принадлежащая к L по α и зависящая только от разностей x(t2, α)-х(t1, α); тогда для любого t1 и почти всех α
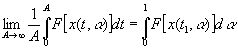(10.16)
Это эргодическая теорема Биркгоффа, доказанная некогда автором и другими.
В упомянутой статье из "Acta Mathematica" установлено, что если U - действительное унитарное преобразование функции K(t), то
, (10.17)
где β отличается от α только сохраняющим меру преобразованием интервала (0, 1) в себя.
Пусть теперь К(t) принадлежит к L, и пусть
(10.18)
в смысле Планшереля. Рассмотрим действительную функцию
, (10.19)
изображающую отклик линейного преобразователя на броунов вход. Она будет иметь автокорреляцию
, (10.20)
[c.282]
которая, в силу эргодической теоремы, почти для всех значений α будет равна
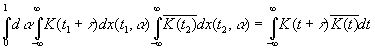(10.21)
Тогда спектр почти всегда будет равен
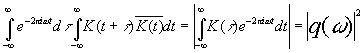(10.22)
Но это истинный спектр. Выборочная автокорреляция за время усреднения А (в нашем случае 2700 сек) будет равна
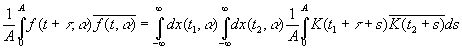(10.23)
В результате выборочный спектр почти всегда будет иметь временно́е среднее
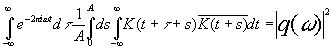(10.24)
Следовательно, выборочный спектр и истинный спектр будут иметь одно и то же среднее значение по времени.