24. Выборочный коэффициент корреляции
Выборочный коэффициент корреляции является одним из основных показателей тесноты связи между двумя переменными. При изучении зависимости переменной Y от переменной Х выборочный коэффициент корреляции обозначается как rxy. При изучении зависимости переменной Х от переменной Y выборочный коэффициент корреляции обозначается как ryx.
Выборочный коэффициент корреляции является оценкой коэффициента корреляции Pxy генеральной совокупности.
Выборочный парный коэффициент корреляции ryx:
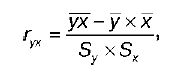
где ух - среднее арифметическое произведения факторной и результативной переменных:

S y – выборочное среднеквадратическое отклонение результативной переменной у , показывающее, на сколько единиц в среднем отклоняются значения результативной переменной у от ее среднего значения y-:
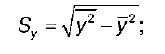
у 2 – среднее значение из квадратов значений результативной переменной у :
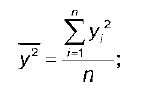
y2 – квадрат средних значений результативной переменной у :
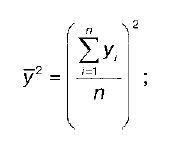
S x – выборочное среднеквадратическое отклонение факторной переменной х, показывающее, на сколько единиц в среднем отклоняются значения факторной переменной х от ее среднего значения x :
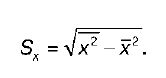
Выборочный коэффициент корреляции обладает следующими свойствами:
1) по абсолютной величине выборочный коэффициент корреляции не превосходит единицы: | r yx | ≤ 1, или –1 ≤ ryx ≤ 1;
2) если ryx = 0, т. е. выборочный коэффициент корреляции равен нулю, то переменные Y и Х не связаны статистической зависимостью. В этом случае проведение регрессионного анализа между исследуемыми переменными считается нецелесообразным;
3) если |ryx| = 1, т. е. выборочный коэффициент корреляции по абсолютной величине равен единице, то наблюдаемые значения исследуемых переменных связаны линейной функциональной зависимостью;
4) `если выборочный коэффициент корреляции принадлежит интервалу от нуля до единицы, то связь между исследуемыми переменными прямая; если же выборочный коэффициент корреляции принадлежит интервалу от нуля до минус единицы, то связь между исследуемыми переменными обратная.
25. Выборочное корреляционное отношение. Свойства выборочного корреляционного отношения
Выборочное корреляционное отношение является основным показателем при оценке тесноты нелинейной корреляционной связи между двумя переменными Y и Х. При изучении зависимости переменной Y от переменной Х выборочное корреляционное отношение обозначается как ηyx.
При изучении зависимости переменной Х от переменной Y выборочное корреляционное отношение обозначается как ηxy.
Выборочным корреляционным отношением
Y к Х называется отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению переменной Y:
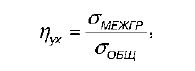
где Gмежгр – это межгрупповое среднее квадратическое отклонение переменной Y:
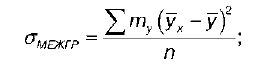
G общ – это общее среднее квадратическое отклонение переменной Y:
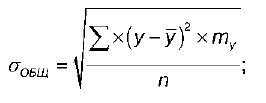
где n – объем выборки (сумма всех частот);
m х – частота значениях переменной X;
m – частота значения у переменной Y;
у – среднее значение переменной Y;
у х – условная средняя переменной Y.
Выборочным корреляционным отношением X
к Y называется отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению переменной Х:
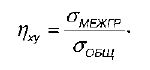
Выборочное корреляционное отношение обладает следующими свойствами:
1) значение выборочного корреляционного отношения принадлежит интервалу от нуля до единицы включительно:
0 ≤ η yx ≤ 1;
2) если η yx = 0, т. е. значение выборочного корреляционного отношения равно нулю, то между исследуемыми переменными Y и Х корреляционная зависимость отсутствует;
3) если η yx = 1, т. е. значение выборочного корреляционного отношения равно единице, то между исследуемыми переменными Y и Х существует функциональная зависимость;
4) выборочное корреляционное отношение не меньше абсолютной величины выборочного коэффициента корреляции:
![]()
5) если выборочное корреляционное отношение равно абсолютной величине выборочного коэффициента корреляции, т. е. если ![]()
то между исследуемыми переменными существует точная линейная корреляционная зависимость. Основным достоинством выборочного корреляционного отношения η yx по сравнению с выборочным коэффициентом корреляции r yx является то, что показатель выборочного корреляционного отношения можно использовать как меру тесноты любой формы связи.
26. Общая модель парной регрессии
Предположим, что в результате статистического наблюдения были получены данные, характеризующие две переменные – Х и Y. С помощью корреляционного анализа было доказано наличие взаимосвязи между данными переменными. Следующим этапом исследования является задача определения точного вида выявленной зависимости между переменными с помощью регрессионного анализа.
Регрессионный анализ – это определение аналитического выражения связи или вида функции, в которой изменение одной величины (результативной переменной) обусловлено влиянием независимой величины (факторной переменной). Регрессионное уравнение, или регрессионная функция, количественно характеризует данную взаимосвязь.
Базисная регрессионная модель – это модель парной, или однофакторной, регрессии, в которой участвуют одна факторная и одна результативная переменные. Модель однофакторной регрессии называется полиномом первой степени и используется для описания равномерно развивающихся во времени процессов.
Модель парной регрессии зависимости результативной переменной у от факторной переменной х в общем виде записывается следующим образом:
yi = в0 + в1xi + ε i ,
где yi – значения результативной переменной, /= 1 ,n;
хi - значения факторной переменной, /= 1 ,n;
в 0, в 1 – неизвестные параметры модели парной регрессии;
n – количество наблюдений.
Модель парной регрессии зависимости результативной переменной х от факторной переменной у в общем виде записывается следующим образом:
хi = в0 + в1уi + ε i .
Параметр ε i модели парной регрессии называется случайной ошибкой модели. Появление случайной ошибки в модели регрессии обусловлено следующими объективными предпосылками:
1) существованием вероятности того, что переменные, участвующие в модели, могут быть измерены с ошибкой.
2) включение в модель парной регрессии только одной факторной переменной, которая не способна полностью объяснить вариацию результативной переменной.
Вид функции регрессии , т. е. аналитическую форму зависимости между результативной и факторной переменными, можно определить двумя методами.
1. Путем визуальной оценки характера связи. На линейном графике по оси абсцисс откладываются значения факторной переменной х, по оси ординат – значения результативной переменной у. На пересечении соответствующих значений отмечаются точки. Полученный точечный график в указанной системе координат называется корреляционным полем. Если соединить полученные точки, то полученная линия будет называться эмпирической.
2. Путем теоретического и логического анализа природы изучаемых явлений, их социально-экономической сущности.
Параметр в 1 уравнения парной регрессии называется коэффициентом регрессии . Его величина показывает, насколько в среднем изменится результативный признак у при изменении факторного признака х на единицу своего измерения. Знак параметра β1 в уравнении парной регрессии указывает на направление связи между переменными: