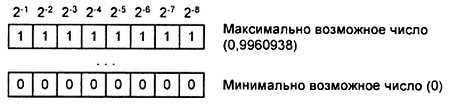
Рис. 4.11.Формат 8-разрядного дробного беззнакового двоичного кода
Или договоримся, что она находится точно посередине кода, и тогда мы сможем записывать числа, содержащие как целую, так и дробную части. Формат такого 8-разрядного беззнакового двоичного кода приведен на рис. 4.12. На рисунке приведены два числа, записанных в этом коде.
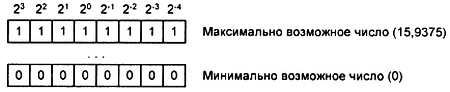
Рис. 4.12.Формат 8-разрядного смешанного беззнакового двоичного кода
Остальные виды двоичных кодов, используемых для представления чисел с фиксированной запятой, рассматривать не будем. Они строятся точно так же, как и для целых чисел.
Представление рациональных чисел в двоичном коде с плавающей запятой
Часто приходится обрабатывать очень большие числа (например, расстояние между звездами) или, наоборот, очень маленькие числа (например, размеры атомов или электронов). При таких вычислениях пришлось бы использовать числа с фиксированной запятой очень большой разрядности. В то же время нам не нужно знать расстояние между звездами с точностью до миллиметра. Для вычислений с такими величинами числа с фиксированной запятой неэффективны.
В десятичной арифметике в таких случаях число записывается в виде мантиссы, умноженной на 10 в степени, отображающей порядок числа, например:
2∙10; 1,6∙10.
В алгебре такое представление рациональных чисел называют стандартным видом числа. В двоичной арифметике тоже используется похожая форма записи чисел - представление с плавающей запятой (часто также называемое представлением с плавающей точкой).
А теперь рассмотрим промышленные стандарты, используемые для представления чисел с плавающей запятой в компьютерах. Существует стандарт IEEE 754 для представления чисел с одинарной точностью (float) и с двойной точностью (double). Для записи числа в формате с плавающей запятой одинарной точности требуется 32-битовое слово.
Для записи чисел с двойной точностью требуется 64-битовое слово. Чаще всего числа хранятся в нескольких соседних ячейках памяти процессора. Форматы одинарной точности и удвоенной точности числа с плавающей запятой приведены на рис. 4.13.
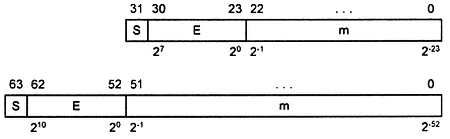
Рис. 4.13.Форматы чисел с плавающей запятой
На рис. 4.13 над полями числа с плавающей запятой показан номер двоичного разряда, а внизу двоичный вес каждого разряда. При этом буквой S обозначен знак числа, 0 - это положительное число, 1 - отрицательное число, е обозначает смещенный порядок числа. Смещение требуется, чтобы не вводить в число еще один знак. Смещенный порядок - всегда положительное число. В формате одинарной точности для порядка выделено 8 битов. Для смещенного порядка двойной точности отводится 11 битов. Для формата одинарной точности принято смещение 127, а для формата двойной точности - 1023. В десятичной мантиссе числа стандартного вида старший разряд - это цифра от 1 до 9. Старший разряд двоичной мантиссы - всегда 1. Поэтому для хранения старшей единицы двоичной мантиссы не выделяется отдельный бит. Единица подразумевается, как и запятая, отделяющая дробную часть от целой. Кроме того, в формате чисел с плавающей точкой принято, что мантисса всегда больше 1. То есть значения мантиссы лежат в диапазоне от 1 до 2.
Рассмотрим несколько примеров.
1. Определить число с плавающей запятой, лежащее в четырех соседних байтах:
11000001 01001000 00000000 00000000.
• Знаковый бит, равный 1, показывает, что число отрицательное.
• Экспонента 10000010 в десятичном виде соответствует числу 130. Вычтя число 127 (смещение) из 130, получим число 3.
• Теперь запишем мантиссу с учетом неявной единицы:
100 1000 0000 0000 0000 0000 1,1001
• И, наконец, определим десятичное число: 1100,12 = 12,510.
2. Определить число с плавающей запятой, лежащее в четырех соседних байтах:
11000011 00110100 00000000 00000000.
• Знаковый бит, равный 1, показывает, что число отрицательное.
• Экспонента 10000110 в десятичном виде соответствует числу 134. Вычтя число 127 из 134, получим число 7.
• Теперь запишем мантиссу:
011 0100 0000 0000 0000 0000 1,01101.
• И, наконец, определим десятичное число: 101101002 = 18010.
Для того чтобы записать ноль, достаточно записать в смещенный порядок число 000000002. Значение мантиссы при этом не имеет значения. Число, в котором все байты равны 0, тоже попадает в этот диапазон значений.
Бесконечность соответствует смещенному порядку 11111112 и мантиссе, равной 1,0. При этом существует минус бесконечность и плюс бесконечность (переполнение и антипереполнение), которые часто отображаются на экране монитора как +INF и - INF.
При таком значении порядка все остальные комбинации битов в мантиссе (в том числе и все единицы) воспринимаются как не числа и отображаются на экране как NaN.
Представление десятичных чисел
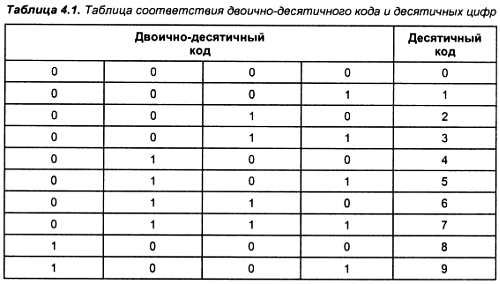
Иногда бывает удобно хранить числа в памяти процессора в десятичном виде (например, для вывода на экран дисплея или при финансовых расчетах). Для представления таких чисел используются двоично-десятичные коды. Цифра одного десятичного разряда представляется при помощи четырех двоичных битов, называемых тетрадой. Иногда встречается название, пришедшее из англоязычной литературы, - нибл. При помощи четырех битов можно закодировать шестнадцать цифр. Лишние комбинации в двоично-десятичном коде являются запрещенными. Таблица соответствия двоично-десятичного кода и десятичных цифр приведена в табл. 4.1.
Остальные комбинации двоичного кода в тетраде являются запрещенными.
Запишем пример двоично-десятичного кода:
1258 = 0001 0010 0101 1000
589 = 0000 0101 1000 1001
Достаточно часто в памяти процессора для хранения одной десятичной цифры выделяется одна ячейка памяти (8-, 16- или 32-разрядная). Это делается для повышения скорости работы программы. Для того чтобы отличить такое представление двоично-десятичного числа от стандартного, последнее называют упакованной формой двоично-десятичного числа.
Суммирование двоично-десятичных чисел
Суммирование двоично-десятичных чисел можно производить по правилам обычной двоичной арифметики, а затем производить двоично-десятичную коррекцию, заключающуюся в проверке каждой тетрады на допустимость ее кода. Если в какой-либо тетраде обнаруживается запрещенная комбинация или был перенос в старшую тетраду, то это говорит о переполнении. В этом случае необходимо произвести двоично-десятичную коррекцию. Двоично-десятичная коррекция заключается в дополнительном суммировании числа 6 (число запрещенных комбинаций) с тетрадой, в которой произошло переполнение. Приведем два примера использования двоично-десятичной коррекции. Просуммируем десятичное число 18, записываемое в двоично-десятичном коде как 0001 1000 и десятичное число 13, двоично-десятичный код 0001 0011. Ожидаемый результат 31. Запишем наши действия в столбик, как это показано на рис. 4.14.
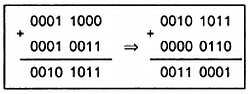
Рис. 4.14.Суммирование чисел 18 и 13 в двоично-десятичном коде
В результате выполнения двоичного суммирования получим число 0010 1011 (2B16). To есть младшая тетрада содержит запрещенную комбинацию. Это означает, что необходимо выполнить десятичную коррекцию. Прибавим к младшей тетраде код коррекции 6. Эта операция показана на рис. 4.14 в столбике, записанном справа. В результате второго двоичного суммирования получаем результат 31. То есть именно то, что и ожидалось!
Во втором примере просуммируем два десятичных числа 19, записываемых в двоично-десятичном коде как 0001 1001. Ожидаемый результат 38.
Запишем наши действия в столбик, как это показано на рис. 4.15.
В результате выполнения двоичного суммирования получим число 0011 0010 (32). В этом случае запрещенных комбинаций нет. Но зато был перенос в старшую тетраду, т. е. и в этом случае необходимо выполнить десятичную коррекцию. Прибавим к младшей тетраде код коррекции 6.
Эта операция показана на рис. 4.15 в столбике, записанном справа. В результате второго двоичного суммирования получаем результат 38. То есть именно то, что и ожидалось! Работа со старшей тетрадой ничем не отличается от работы с младшей тетрадой, рассмотренной в приведенных примерах.