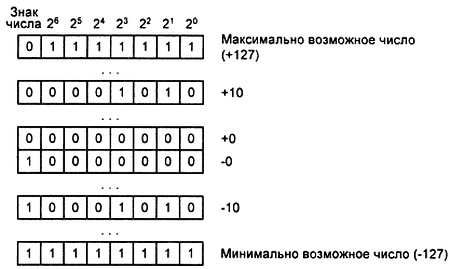
Рис. 4.2.Формат 8-разрядного прямого знакового двоичного кода
Диапазон 8-разрядных целых чисел, которые можно записать, пользуясь таким кодом, простирается от -127 до +127. Для 16-разрядного числа этот диапазон составит от -32767 до +32767. В 8-разрядном процессоре для хранения такого числа используются две ячейки памяти, расположенные в соседних адресах.
Недостатком прямого знакового кода является то. что знаковый разряд и цифровые разряды приходится обрабатывать раздельно. Алгоритм программ, работающих с такими кодами, получается сложный. Для выделения и изменения знакового разряда приходится применять механизм маскирования разрядов, что резко увеличивает размер программы и уменьшает ее быстродействие. Для того чтобы алгоритм обработки знакового и цифровых разрядов не различался, были введены обратные двоичные коды.
Знаковые обратные двоичные коды
Обратные двоичные коды отличаются от прямых только тем, что отрицательные числа в них получаются инвертированием всех разрядов положительного числа. При этом обработка знакового и цифровых разрядов не различается. Алгоритм работы с такими кодами резко упрощается.
Тем не менее, при работе с обратными кодами требуется специальный алгоритм распознавания знака, вычисления абсолютного значения числа и восстановления знака результата числа. Кроме того, в прямом и обратном коде для представления числа 0 используются два разных кода, тогда, как известно, что число 0 положительное и отрицательным не может быть никогда. Формат 8-разрядного обратного знакового двоичного кода приведен на рис. 4.3. На рисунке приведено шесть различных чисел, записанных в этом коде.
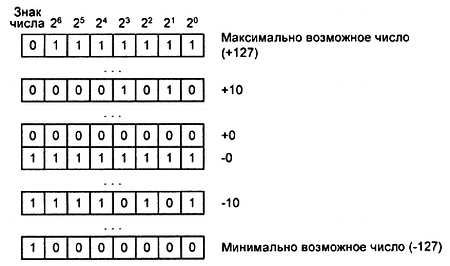
Рис. 4.3. Формат 8-разрядного обратного знакового двоичного кода
Знаковые дополнительные двоичные коды
От перечисленных недостатков свободны дополнительные коды. Они позволяют суммировать положительные и отрицательные числа, не анализируя знаковый разряд, и при этом получать правильный результат. Все это становится возможным благодаря тому, что дополнительные числа являются естественным кольцом чисел, а не искусственным образованием, как прямые и обратные коды. Кроме того, немаловажным является то обстоятельство, что вычислять дополнение в двоичном коде чрезвычайно легко. Для этого достаточно к обратному коду добавить 1.
Формат 8-разрядного дополнительного знакового двоичного кода приведен на рис. 4.4. На рисунке приведено шесть различных чисел, записанных в этом коде.
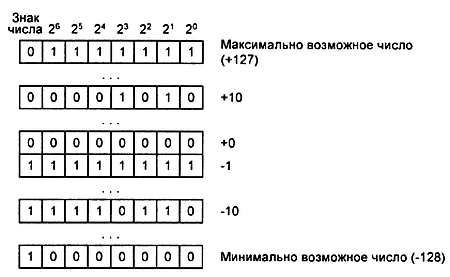
Рис. 4.4.Формат 8-разрядного дополнительного знакового двоичного кода
Числа, которые можно представлять 8-разрядным дополнительным двоичным кодом, находятся в диапазоне от -128 до +127. Для 16-разрядного кода этот диапазон будет от -32768 до +32767. В 8-разрядном процессоре для хранения 16-разрядного числа используются две ячейки памяти, расположенные в соседних адресах.
В обратных и дополнительных кодах наблюдается интересная особенность, которая называется эффектом распространения знака: при преобразовании однобайтного числа в двухбайтное достаточно всем битам старшего байта присвоить значение знакового бита исходного байта. То есть для хранения знака числа можно использовать сколько угодно старших битов. При этом значение кода совершенно не изменяется. Эффект распространения знака используется при подключении таких устройств, как АЦП или ЦАП, к микропроцессору если их разрядности не совпадают.
Использование для представления знака числа двух битов предоставляет интересную возможность контролировать возникновение переполнения при выполнении арифметических операций. В качестве второго знакового бита используется флаг переноса С. Можно конечно использовать и большее количество знаковых битов, но это никаких дополнительных преимуществ не дает.
Рассмотрим несколько примеров работы с дополнительными двоичными кодами.
1. Просуммируем числа +12 и +5. Суммирование этих чисел в двоичном и десятичном представлении приведено на рис. 4.5.
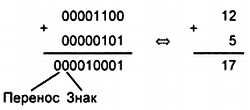
Рис. 4.5. Суммирование чисел +12 и +5
В этом примере видно, что в результате суммирования получается правильный результат. Это можно проконтролировать по флагу переноса С, который совпадает со знаком результата (эффект распространения знака действует).
2. Просуммируем два отрицательных числа -12 и -5. Суммирование этих чисел в двоичном и десятичном представлении приведено на рис. 4.6.
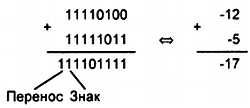
Рис. 4.6.Суммирование чисел -12 и -5
В этом примере флаг переноса С тоже совпадает со знаком результата, т. е. переполнения не произошло и в этом случае.
3. Просуммируем положительное и отрицательное числа -12 и +5. Суммирование этих чисел в двоичном и десятичном представлении приведено на рис. 4.7.
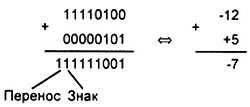
Рис. 4.7.Суммирование чисел -12 и +5
В этом примере при суммировании положительного и отрицательного числа автоматически получается правильный знак результата. В данном случае знак результата отрицательный. Флаг переноса совпадает со знаком результата, поэтому переполнения не было (мы можем убедиться в этом непосредственными вычислениями на бумаге или на калькуляторе).
4. Просуммируем положительное и отрицательное числа +12 и -5. Суммирование этих чисел в двоичном и десятичном представлении приведено на рис. 4.8.
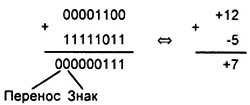
Рис. 4.8.Суммирование чисел +12 и -5
В данном примере знак результата положительный. Флаг переноса совпадает со знаком результата, поэтому переполнения не было и в этом случае.
5. Просуммируем числа +100 и +31. Суммирование этих чисел в двоичном и десятичном представлении приведено на рис. 4.9.
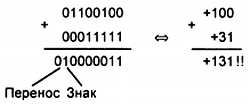
Рис. 4.9. Суммирование чисел +100 и +31
В этом примере видно, что в результате суммирования произошло переполнение 8-битовой переменной, т. к. в результате операции над положительными числами получился отрицательный результат. Если рассмотреть флаг переноса С, то он не совпадает со знаком результата. Эта ситуации является признаком переполнения результата и легко обнаруживается при помощи операции "исключающее ИЛИ" над старшим битом результата и флагом переноса С. Большинство процессоров осуществляют эту операцию аппаратно и помещают результат во флаг переполнения OV.
6. Просуммируем числа -100 и -31. Суммирование этих чисел в двоичном и десятичном представлении приведено на рис. 4.10.
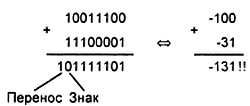
Рис. 4.10.Суммирование чисел -100 и -31
В этом примере операции над отрицательными числами в результате суммирования произошло переполнение 8-битовой переменной, т. к. получился положительный результат. И в этом случае если рассмотреть флаг переноса С, то он не совпадает со знаком результата. Отличие от предыдущего случая только в комбинации этих битов. В примере 5 говорят о переполнении результата (комбинация 01), а в примере 6 - об антипереполнении результата (комбинация 10).
Представление рациональных чисел в двоичном коде с фиксированной запятой
Кроме целых чисел, часто требуется работать с рациональными числами. Как и в случае целых чисел, рациональные числа могут быть беззнаковыми и знаковыми. Для двоичного представления знаковых рациональных чисел могут быть использованы прямые, обратные и дополнительные коды. Принцип их построения точно такой же, как и в случае целых чисел.
Рассмотрим, как можно записать рациональное число. Ранее, рассматривая целые числа, мы предполагали, что в двоичном числе запятая, разделяющая целую и дробную части, находится правее самого младшего разряда. Но кто сказал, что она должна всегда находиться именно в этом месте? Мы можем договориться, что запятая, разделяющая целую и дробную части двоичного числа, находится слева от самого старшего разряда, и тогда в такой переменной можно будет записывать только дробные числа, меньшие 1,010. Формат 8-разрядного дробного беззнакового двоичного кода приведен на рис. 4.11. На рисунке приведены два числа, записанных в этом коде.