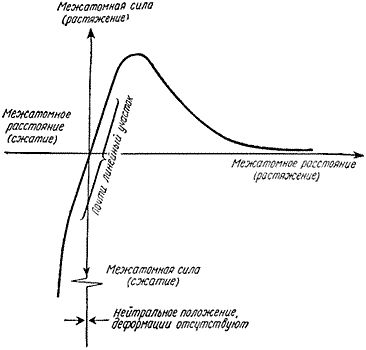
Рис. 3. Зависимость силы, действующей междудвумя атомами, от расстояния между ними.
При очень больших деформациях - скажем 5–10% - от пропорциональностимежду напряжениями и деформациями не остается и следа. Но обычно деформациине превышают ±1%, а в этом диапазоне зависимость между напряжениями и деформациямилинейна. Кроме того, для малых деформаций процесс нагрузки и разгрузкиобратим, то есть кусок материала можно нагрузить и снять с него нагрузкутысячи и миллионы раз с одним и тем же результатом. Наглядный пример этому- пружинка балансира в часах, которая повторяет этот процесс 18 000 разв час. Такой тип поведения твердого тела под нагрузкой называется упругим.Упругое поведение свойственно большинству технических материалов, хотясуществуют и материалы с пластическим поведением. Наиболее ярко пластичностьпроявляется у таких веществ, как пластилин, оконная замазка - эти материалыне подчиняются закону Гука: после снятия внешних нагрузок их форма и размерыне восстанавливаются.
Вообще говоря, наука об упругости изучает напряжения и деформации втвердых телах. Не только во времена Гука, но даже и совсем недавно мы малознали об упругих свойствах материалов. В тех случаях, когда их деформациипревышали примерно 1%, они либо разрушались, либо утрачивали упругие свойства.Поэтому кривая зависимости межатомной силы от расстояния при больших смещенияхатомов из положения равновесия (рис. 3) представляла главным образом академическийинтерес, на практике больших напряжений достигнуть не удавалось. И лишьсравнительно недавно появилась возможность растянуть очень прочные нитевидныекристаллы - усы - до деформаций от 3 до 6%. Эти опыты подтвердили, чтозакон Гука не всегда верен. Зависимость напряжения от деформации на графикеотклоняется от прямой линии и следует кривой межатомной силы, которая быларассчитана ранее физиками-теоретиками. На рис. 4 показана такая криваядля кремниевого уса, деформированного более чем на 3%.
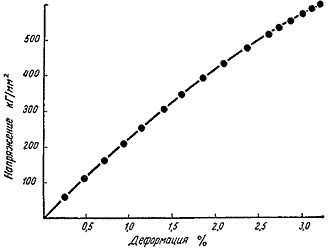
Рис. 4. Кривая напряжение-деформацияочень кремниевого кремниевого уса, который был деформирован в испытательноймашине до 3,6%. Поведение уса при больших деформациях не подчиняется законуГука.
Модуль Юнга
Гук установил, что удлинения, укорочения, прогибы как пружин, так идругих упругих тел пропорциональны приложенным к ним нагрузкам. Они зависят,конечно, от геометрических размеров и формы конструкции, а также от того,из какого материала она сделана. Мы не знаем, понимал ли Гук, в чем разницамежду упругостью как свойством материала и упругостью как функцией формыи размеров конструкции. Дело в том, что можно получить сходные кривые "нагрузка- удлинение" и для куска резинового шнура, и для завитого куска стали,который мы называем пружиной, - это сходство явилось источником бесконечныхзаблуждений. Примерно столетие после Гука существовала эта путаница: невсем была ясна разница между двумя понятиями упругости.
Около 1800 года Томас Юнг (1773–1829) пришел к выводу,что, если пользоваться не абсолютными значениями сил и смещений в конструкциях,а напряжениями и деформациями, то закон Гука можно записать в следующемвиде:Напряжение / Деформация = σ/ε константа.
Юнг заключил, что эта константа является неотъемлемой характеристикойкаждого химического вещества и представляет его жесткость. Мы называемэту константу упругости модулем Юнга и обозначаем буквой E. Итак,E = σ/ε
Следовательно, Е описывает жесткость материала как такового. Жесткостьлюбого заданного объекта зависит не только от модуля Юнга материала, но и отгеометрической формы объекта. Между прочим, считают, что Юнг "был человекомвеликой учености, но, к сожалению, он никогда даже не подозревал, чтовозможности заурядного ума ограничены". Его идея о модуле упругости была изложена в неочень понятной статье, опубликованной в 1807 году. К этому времени Юнгузапретили читать лекции в Королевском институте, так как считали, что онслишком далек от практики. Так и случилось, что одно из самых распространенныхныне и полезных технических понятий не было принято и внедрено в инженернуюпрактику при жизни автора.
Громадная важность модуля упругости для техники объясняется двумя причинами.Во-первых, нам нужно точно знать возникающие под нагрузками смещения как вконструкции в целом, так и в различных ее частях. Разнообразие конструкцийогромно - мосты, самолеты, коленчатые валы и т.д. Посмотрите, например, надеформированное крыло самолета (рис. 5). Под действием рабочих нагрузоквзаимодействие деталей в конструкции не должнонарушаться. В таких расчетах нам в первую очередь нужны величины Е.
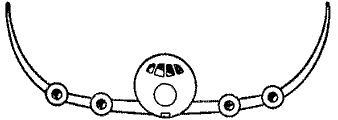
Рис. 5. Самолет, в котором деформация лонжеронов крыла составляет 1,6%(радиус кривизны балки = Толщина / [2xДеформация])
Во-вторых, хотя неспециалисту и позволено думать, что жесткости всехконструкционных материалов практически одинаковы и говорить "Отлично, этовполне жестко! Не видно никаких смещений", такие суждения не соответствуютдействительному положению вещей. Нам необходимо знать модули упругостиразличных материалов (стали, древесины и т.д.) не только для того, чтобырассчитать деформации конструкции, но и для того, что бы деформации ееотдельных элементов были согласованными - тогда и напряжения между этимиэлементами будут распределяться так, как мы хотели этого, проектируя конструкцию.Определяя модуль Юнга, мы разделили напряжение на безразмерное число -деформацию, следовательно, модуль должен иметь размерность напряжения (кг/мм,Н/м и т.п.). Если деформация равна 1 (100%), то напряжение оказывается равным модулю упругости. Стало быть,модуль упругости можно считать таким напряжением, которое удваивает длинуупругого образца (конечно, если он прежде не разрушится). Легко себе представить,что величина модуля упругости должна быть большой, обычно она по крайнеймере в 100 раз больше разрушающего напряжения: ведь мы упоминали уже, чтоматериалы, как правило, разрушаются, когда их упругая деформация не превышает1%. Модуль Юнга для стали, например, составляет около 20000 кг/мм.
Как мы уже говорили, величина E может сильно из меняться от одного веществак другому. Ниже приведены величины модуля для некоторыхматериалов.
Материал / Е, кг/мм
Резина / 0,00007x10 (т.е. 0,7)
Неармированные пластики / 0,015x10
Органические молекулярные кристаллы, фталоцианин / 0,015x10
Древесина / 0,15x10
Кость / 0,3x10
Магний / 0,4x10
Обычное стекло / 0,7x10
Алюминий / 0,8x10
Сталь / 2x10
Окись алюминия (сапфир) / 4x10
Алмаз / 12x10
Таким образом, модуль самого жесткого из твердых тел (алмаза) почтив 200 000 раз больше модуля резины, тоже твердого тела. У резин модульупругости очень мал, потому что резина состоит из длинных гибких молекулярныхцепочек, которые в ненагруженном материале изгибаются, свиваются, сплетаются,словом, ведут себя подобно ниткам в спутанном клубке. Когда резину растягивают,изогнутые цепочки распрямляются, и совершенно очевидно, что необходимаядля этого сила будет намного меньше той, которая потребовалась бы, чтобырастянуть пучок нитей, вытянутых в одном направлении. Совершенно иная картинанаблюдается в кристалле. Прикладывая к нему силу, мы действуем непосредственнона межатомные связи, и единственная причина большой разницы в величинеЕдля разных кристаллов заключена в различной жесткости самих химическихсвязей. Наклон прямого участка кривой межатомного взаимодействия оченьсильно зависит от энергии межатомной связи. Но общая форма кривой для всехкристаллов одинакова.