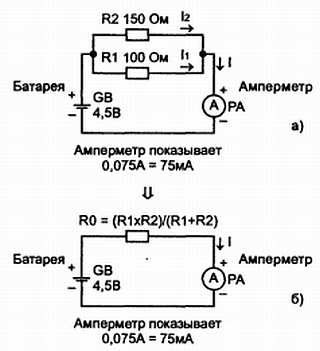
Рис. 2.19.Из которого можно сделать вывод, что при параллельном соединении резисторов общее сопротивление цепи меньше наименьшего сопротивления одного из резисторов цепи
Для трех параллельно соединенных резисторов:
1/R0 = 1/R1 + 1/R2 + 1/R3 (2.10, в)
А теперь включите миллиамперметр в цепь первого резистора (рис. 2.20, а), верхний предел должен быть примерно 50 мА. Когда подключите все элементы схемы, подключите батарею. Прибор покажет силу тока I1 = 45 мА. Отключите батарею и подключите миллиамперметр в цепь второго резистора (рис. 2.20, б). Подключите батарею и замерьте силу тока: прибор покажет I2 = 30 мА.
А теперь сравните все три показания миллиамперметра: сумма сил токов через резисторы R1 и R2 равна силе тока в общей цепи (силе тока, потребляемой от батареи). Отсюда вывод, при параллельном соединении резисторов сила тока в общей (неразветвленной) цепи равна сумме сил токов, протекающих через резисторы.
I0 = I1 + I2. (2.11, а)
Если параллельно соединены три резистора, тогда:
I0 = I1 + I2 + I3. (2.11, б)
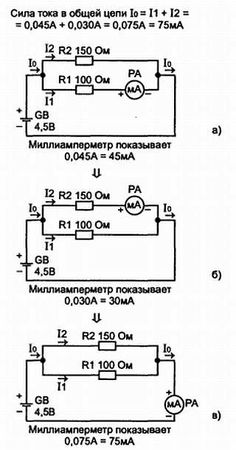
Рис. 2.20.Из которого можно сделать вывод, что сумма силы токов в ветвях (при параллельном соединении) равна силе тока, потребляемого от источника (силе тока в неразветвленной части цепи)
Теперь переключите прибор для измерения напряжения, соберите схему, как показано на рис. 2.21, и замерьте напряжение вначале на резисторе R1, затем на резисторе R2. Вы убедились, что вольтметр в обоих случаях показывает одно и то же напряжение, равное напряжению на зажимах батареи, т. е. 4,5 В? Отсюда вывод: при параллельном соединении резисторов падения напряжения на них равны.
U1 = U2. (2.12, а)
Для трех параллельно соединенных резисторов
U1 = U2 = U3. (2.12, б)
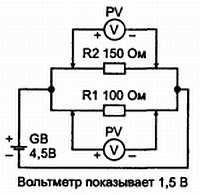
Рис. 2.21.Который позволяет быстро определить, что при параллельном соединении резисторов напряжение на них одинаковое
Часто в вашей практике (при изготовлении какого-либо прибора, устройства) встречаются или могут встретиться такие случаи, когда отсутствует резистор необходимого номинала. Есть два выхода из этого положения.
1. Найти два резистора, желательно одинакового номинала, чтобы сумма их сопротивлений была равна сопротивлению заменяемого резистора. Эти резисторы надо соединить последовательно (2.8).
2. Резисторы можно соединить и параллельно. Для этого следует подобрать один резистор R1, который образует вместе с другим параллельно соединенным резистором R2 заданное сопротивление R0. Если учесть, что номинальные значения сопротивлений постоянных резисторов образуют не непрерывный ряд (смотри табл. 2.2), а в ваших запасах отсутствуют резисторы многих номиналов, входящих в шкалу номинальных значений, то задачу по отысканию второго резистора нельзя отнести к легким. Вы в этом скоро убедитесь. Ускорить и облегчить решение задачи по подбору второго резистора можно с помощью диаграммы, изображенной на рис. 2.22.

Рис. 2.22. Сетка для подбора второго резистора при параллельном соединении резисторов
С помощью этой номограммы можно определить электрические величины двух параллельно соединенных резисторов или катушек индуктивности, а также двух последовательно соединенных конденсаторов.
При определении электрических величин соединяемых резисторов, катушек индуктивности или конденсаторов сопротивления, индуктивности или емкости которых имеют один порядок, пользуются шкалами ОА, ОВ, ОС, а если их значения различаются на один порядок, то шкалами ОА, OD, ОЕ.
Пример 1. Параллельно соединены два резистора с номиналами 7,5 кОм и 5 кОм. Прикладывая край линейки к делениям 7,5 на шкале ОА и к 5 - на шкале ОВ, на шкале ОС считываем результат - 3. Общее с сопротивление резисторов будет 3 кОм.
Пример 2. Подобрать два резистора с номиналами одного порядка, общее сопротивление которых при параллельном соединении составило бы 35 Ом.
Деления с числом 35 на шкале ОС нет, поэтому пользуются делением 3,5, помня при этом, что полученный результат надо будет умножить на 10. Сопротивления резисторов находят по шкале ОА и ОВ и выбирают наиболее приемлемый вариант.
Чтобы построить такую номограмму, надо стороны ОА и ОВ равнобедренного треугольника АОВ разделить на 10 равных частей, а биссектрису ОС - на 5 частей. Отсчет ведут от точки О. Каждое деление можно разделить еще на 10 или 5 частей. Угол АОВ может быть любым.
Участок АЕ = (1/10) АВ, а шкала ОЕ, используемая в тех случаях, когда исходные и определяемые электрические величины различаются между собой на один порядок, должна быть разделена на 9,1 части. Значения делений шкалы ОА останутся без изменений, а цена делений шкалы ОВ увеличится в 10 раз.
На рис. 2.23 показан "ключ" пользования диаграммой.

Рис. 2.23.Подбор второго резистора к 150-омному резистору для получения результирующего сопротивления, равного 120 Ом
На практике редко встречаются случаи, когда можно встретить либо только последовательное, либо только параллельное соединение сопротивлений. Чаще всего встречается смешанное соединение сопротивлений (рис. 2.24, а). Чтобы вычислить токи и напряжения в схеме, необходимо ее преобразовать либо только к последовательному, либо только к параллельному соединению. На рис. 2.24 надо найти эквивалентное сопротивление R0 параллельно соединенных резисторов R2 и R3, тогда схема будет состоять из двух последовательно соединенных резисторов R1 и R0, что уже не составит труда для вычислений (рис. 2.24, б).
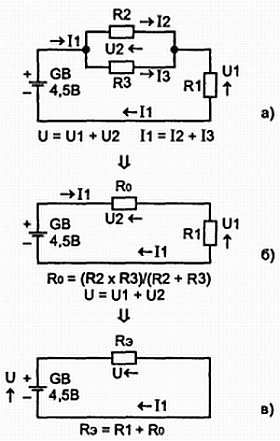
Рис. 2.24.Из которого видно как преобразовать сложную цепь (смешанное соединение резисторов) в простую, позволяющую провести ее расчет
• Решим задачу. На схеме рис. 2.24, а найти силу тока I1, если напряжение источника питания U = 1,5 В, R1 = 100 Ом, R2 = 150 Ом, R3 = 330 Ом.
Решение. Из рис. 2.24, б видно, что сила тока I1 = U/Rэ, a Rэ = R1 + R0.
Определим R0.
R0 = R2∙R3/(R2 + R3) = 150∙330/480 = 103,1 Ом.
Тогда общее сопротивление электрической цепи
Rэ = R1 + R0 = 100 + 103,1= 203,1 Ом,
а сила тока, потребляемая от источника питания
I1 = U/Rэ = 1,5/203,1 ~= 0,0074 А = 7,4 мА.
2.5. ИЗМЕРЕНИЕ СИЛЫ ТОКА, НАПРЯЖЕНИЯ И СОПРОТИВЛЕНИЯ
Прибор для измерения силы тока называется амперметром (миллиамперметром, микроамперметром), а прибор для измерения напряжения (разности потенциалов) - вольтметром (милливольтметром, микровольтметром). Амперметры и вольтметры обычного типа (в отличие от электронных приборов) имеют одинаковое измерительное устройство, называемое гальванометром.
Гальванометры бывают магнитоэлектрической, электромагнитной и других систем. В радиоэлектронике применяются, главным образом, измерительные приборы магнитоэлектрической системы, которые имеют более высокую чувствительность, большую точность результатов измерений и равномерную шкалу (рис. 2.25).