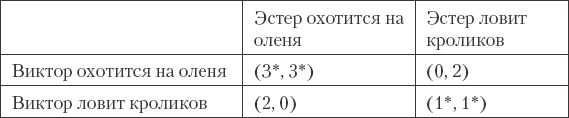
Обратите внимание на то, что есть две ячейки, где обе цифры помечены звездочкой, – это совпадающий лучший выбор обоих игроков. Мы называем такие ячейки "решением игры". Почему? Потому что они показывают сценарии, где ни один из игроков не смог бы сделать лучший выбор. Например, посмотрим на ячейку, в которой оба партнера идут охотиться на оленя (3*, 3*). Если Виктор переключится на кроликов, его выигрыш упадет с 3 баллов до 2, а это не лучший выбор. Эстер получит аналогичный результат. Ячейка (3*, 3*) называется "чистой стратегией" уравнения игры Нэша: ни один из игроков ничего не выиграет, если изменит стратегию.
Другая ячейка решения – (1*, 1*) – тоже считается "чистой стратегией" уравнения игры Нэша, хотя и приносит обоим игрокам меньше баллов. Если Виктор переключится на охоту на оленя, его счет упадет с 1 до 0, а это плохая стратегия. Если Эстер решит сделать то же самое, и для нее это будет плохой выбор.
Теперь, когда мы уяснили основные принципы, давайте посмотрим, что произойдет, если Эстер и Виктор будут многократно играть в эту игру и менять стратегии. Ситуация повторяющейся игры немного напоминает фактические отношения между партнерами, в ходе которых между ними многократно повторяется один и тот же обмен. Например, оба партнера могут выбирать в одной половине случаев охоту на оленя, а в другой – ловлю кроликов. Однако можно найти решение для лучшей повторяющейся стратегии ("смешанной стратегии") и с точки зрения каждого игрока.
Предположим, что Виктор решает охотиться на оленя с вероятностью σоленя ("σ" – вероятность), а наловить кроликов – с вероятностью (1 – σоленя). Тогда, если Виктор охотится на оленя с вероятностью а и ловит кроликов с вероятностью (1 – σоленя), ожидаемый выигрыш (ЕР) для Эстер, если та решит поохотиться на оленя, будет такой:
ЕР для Эстер, если она охотится на оленя = = (3) (σоленя) + (0) (1 – σоленя).
Если Эстер ловит кроликов:
ЕР для Эстер, если она ловит кроликов = (2) (σоленя) + (1) (1 – σоленя).
Теперь, если мы примем, что EPоленя = EPкроликов, действия Виктора окажутся безразличны для выигрыша Эстер в случае изменения им выбора. Поэтому изменение выбора Виктора для Эстер приемлемо (ее точка безразличия будет достигнута):
(3) (σоленя) + (0) (1 – σоленя) = (2) (σоленя) + (1) (1 – σоленя)
3σоленя = 1 + σоленя
2σоленя = 1
σоленя = 1/2.
Следовательно, Эстер не заботит, будет ли Виктор с вероятностью 1/2 охотиться на оленя или ловить кроликов с вероятностью 1/2. Его выбор не повлияет на ее выигрыш. Поэтому смешанная стратегия Виктора может привести к уравнению Нэша для смешанной, а не для чистой стратегии.
В этом уравнении аналогичные вычисления показывают, что смешанная стратегия работает иначе. Для выигрыша Виктора не имеет значения, предпочтет ли Эстер охотиться на оленя с вероятностью 1/2 или ловить кроликов с такой же вероятностью. Поэтому когда каждый игрок выбирает оленя или кроликов с вероятностью 1/2, его выбор описывает уравнение Нэша для смешанной стратегии.
Игры с нулевым результатом
В игре типа "победитель получает всё" каждая ячейка в матрице выигрышей будет включать и победителя, и побежденного. В приведенном ниже примере два игрока одновременно передвигают покерные фишки по столу.

В этой игре нет уравнения Нэша для чистой стратегии – у игроков нет возможности получить максимальную выгоду одновременно.
Давайте взглянем на уравнения смешанной стратегии, где каждый игрок делает свой выбор с определенной вероятностью (мы снова будем исходить из того, что в этой игре много раундов). Игрок подбрасывает монетку, чтобы решить, двигать ему фишку вверх или вниз. В результате он случайным образом выбирает то или иное направление в 50 % случаев. Следовательно, ожидаемый выигрыш при передвижении фишки влево составит:
EPвлево = (0,5) (–3) + (0,5) (1) = –1.
При передвижении фишки вправо ее ожидаемый выигрыш будет равен:
EPвправо = (0,5) (2) + (0,5) (0) = 1.
Поэтому, если игрок подбрасывает монетку, чтобы решить, двигать ему фишку вверх или вниз, он должен выбрать движение фишки вправо в качестве чистой стратегии, потому что в этом случае ожидаемый выигрыш будет выше, чем при передвижении фишки влево. Поскольку он это знает, то не собирается делать рандомизированный выбор, подбрасывая монетку.
Как мы уже видели, анализ с помощью теории игр позволяет воспользоваться алгеброй для создания идеального уравнения Нэша для смешанной стратегии. Снова выявляем точку безразличия соперников среди прочих чистых стратегий. Вероятность того, что игрок ("он") передвинет фишку вверх, становится неизвестной величиной σВверх, которую мы должны определить. Если он будет двигать фишку вверх с вероятностью σВверх, которая уже известна, вниз ему придется двигать фишку с вероятностью (1 – σВверх). Поэтому мы вычисляем ожидаемый выигрыш для другого игрока (для "нее") следующим образом:
ЕРвлево = (σВверх) (–3) + (1 – σВверх) (1) = –4σВверх + 1.
ЕРвправо = (σВверх) (2) + (1 – σВверх) (0) = 2σВверх.
Теперь примем, что ЕРвлево = ЕРвправо, чтобы вычислить значение σВверх, которое сделает ее безразличной к сделанному ею выбору. Вот эти вычисления:
ЕРвлево = ЕРвправо
–4σВверх + 1 = 2σВверх
1 = 6σВверх
σВверх = 1/6.
Обобщим все вышесказанное. Если он двигает фишку вверх с вероятностью 1/6 и вниз с вероятностью 5/6, с точки зрения ожидаемых выигрышей она остается безразличной. Более того, она не может сыграть лучше, передвигая свою фишку влево или вправо, когда он пользуется смешанной стратегией.
Теперь давайте посмотрим на ситуацию с точки зрения ее действий и его выигрышей. Вычислим вероятность того, что она передвинет фишку влево, σВлево и вправо, σВправо, чтобы он был безразличен к ее смешанной стратегии. Начнем с вопроса, какими будут его ожидаемые выигрыши.
ЕРВверх = (σВлево) (3) + (1 – σВлево) (–2) = 5σВлево + 2.
ЕРВниз = (σВлево) (–1) + (1 – σВлево) (0) = -σВлево.
Затем находим вероятность равноценности (indifference probability) σВлево с помощью следующего уравнения:
ЕРВверх = ЕРВниз
5σВлево + 2 = -σВлево
6σВлево = 2
σВлево = 1/3.
Мы обнаружили, что он будет оставаться безразличным к ее смешанной стратегии, если она передвинет фишку влево с вероятностью 1/3, а вправо – с вероятностью 2/3.
Если мы соединим смешанные стратегии обоих игроков, получим уравнение Нэша для смешанной стратегии для игры в целом. Следовательно, даже при условии, что у нас нет уравнения Нэша для чистой стратегии, игра позволяет составить уравнение смешанной стратегии.
Эта стратегия работает и в отношениях, когда партнеры обмениваются с некоторой вероятностью различными поведенческими проявлениями: улыбками, совместным поеданием обеда или предложениями заняться сексом. То, что решение уравнения Нэша для игры может существовать, даже когда чистая стратегия невозможна, открывает большие возможности. Мы можем применить это уравнение к принятию и отклонению предложения заняться сексом с партнером.