Всего за 114.9 руб. Купить полную версию
12. ПОЛУЧЕНИЕ СИНУСОИДАЛЬНОЙ ЭДС. ОСНОВНЫЕ СООТНОШЕНИЯ
Электрические цепи, в которых значения и направления ЭДС, напряжения и тока периодически изменяются во времени по синусоидальному закону, называются цепями синусоидального тока. Иногда их называют просто цепями переменного тока.
Электрические цепи, в которых значения и направления ЭДС, напряжения и тока периодически изменяются во времени по законам, отличным от синусоидального, называются цепями несинусоидального тока.
Генераторы электрических станций переменного тока устроены так, что возникающая в их обмотках ЭДС изменяется по синусоидальному закону. Синусоидальная ЭДС в линейных цепях, где содержатся резистивные, индуктивные и емкостные элементы, возбуждает ток, изменяющийся по закону синуса.
Возникающие при этом ЭДС самоиндукции в катушках и напряжения на конденсаторах, как это вытекает из выражений:
![]()
также изменяются по синусоидальному закону, так как производная синусоидальной функции есть функция синусоидальная. Напряжение на резистивном элементе будет так-же изменяться по синусоидальному закону: u = ir .
Целесообразность технического использования синусоидального тока обусловлена тем, что КПД генераторов, двигателей, трансформаторов и линий электропередачи при синусоидальной форме ЭДС, напряжения и тока получается наивысшим по сравнению с несинусоидальным током. Кроме того, при иных формах изменения тока из(за ЭДС самоиндукции могут возникать значительные перенапряжения на отдельных участках цепи.
Важную роль играет и тот факт, что расчет цепей, где ЭДС, напряжение и ток изменяются синусоидально, значительно проще, чем расчет цепей, где указанные величины изменяются по несинусоидальному закону.
Рассмотрим механизм возникновения и основные соотношения, характерные для синусоидальной ЭДС .
Для этого удобно использовать простейшую модель – рамку, вращающуюся с постоянной угловой скоростью в равномерном магнитном поле. Проводники рамки, перемещаясь в магнитном поле, пересекают его, и в них на основании закона электромагнитной индукции наводится ЭДС. Значение ЭДС пропорционально магнитной индукции B , длине проводника l и скорости перемещения проводника относительно поля υ t : е = Bl υ t .
Выразив скорость υ t через окружающую скорость υ и угол α, получим: е = Bl υ sin α = Em sin α.
Угол α равен произведению угловой скорости рамки ω на время t : α = ω t .
Таким образом, ЭДС, возникающая в рамке, будет равна: е = Em sin α = Em sin ω t .
За один поворот рамки происходит полный цикл изменения ЭДС.
Если при t = 0 ЭДС е не равна нулю, то выражение ЭДС записывается в виде: е = Em sin (ω t + y ),
где e – мгновенное значение ЭДС (значение ЭДС в момент времени t );
Em – амплитудное значение ЭДС (значение ЭДС в момент времени );
![]()
(ω t + ψ) – фаза;
ψ – начальная фаза.
Фаза определяет значение ЭДС в момент времени t , начальная фаза – при t = 0.
Время одного цикла называется периодом T , а число периодов в секунду – частотой f :
![]()
Единицей измерения частоты является c –1, или герц (Гц). Величина
![]()
в электротехнике называется угловой частотой и измеряется в рад/с.
Частота вращения рамки n и частота ЭДС f связаны между собой соотношением:
![]()
откуда
![]()
13. ЦЕПЬ, СОДЕРЖАЩАЯ КАТУШКУ С АКТИВНЫМ СОПРОТИВЛЕНИЕМ R И ИНДУКТИВНОСТЬЮ L
Реальная катушка любого электротехнического устройства обладает определенным активным сопротивлением r и индуктивностью L . Участок цепи с индуктивностью L будем рассматривать как участок, обладающий индуктивным сопротивлением xl . Уравнение напряжений, составленное по второму закону Кирхгофа для цепи с r и L , имеет вид: Ū = Ūr + Ūl .
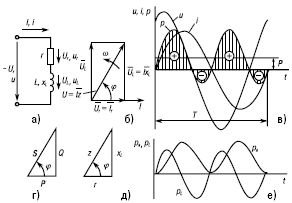
Рис. 15. Цепь, содержащая катушку с активным сопротивлением R и индуктивностью
На векторной диаграмме (рис. 15б) вектор Ur совпадает с вектором тока, а вектор Ul опережает вектор тока на 90°.
Из диаграммы следует, что вектор напряжения сети равен геометрической сумме векторов Urи Ul. Ū = ŪR + ŪL , а его значение
![]()
Выразив напряжения через ток и сопротивления, получим
![]()
Последнее выражение представляет собой закон Ома цепи (рис. 15г):
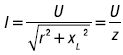
где z – полное сопротивление цепи.
Из векторной диаграммы следует, что напряжение цепи опережает по фазе ток на угол р и его мгновенное значение равно: υ = Um sin (ω t + φ).
Графики мгновенных значений напряжения и тока цепи изображены на рисунке 15в.
Угол сдвига по фазе φ между напряжением и вызванным им током определяют из соотношения:

График pa ( t ) показывает, что активная мощность непрерывно поступает из сети и выделяется в активном сопротивлении в виде теплоты. Она равна: 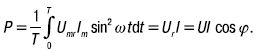
Мгновенная мощность, обусловленная энергией магнитного поля индуктивности, циркулирует между сетью и катушкой. Ее среднее значение за период равно нулю: 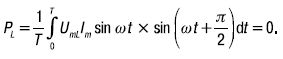
14. ЦЕПЬ, СОДЕРЖАЩАЯ РЕЗИСТИВНЫЙ И ЕМКОСТНОЙ ЭЛЕМЕНТЫ
Участок цепи с емкостью С будем представлять как участок, обладающий емкостным сопротивлением xc .
В этом случае уравнение напряжений цепи (рис. 16а) имеет вид: Ū = Ūr + Ūc
На (рис. 16б) изображена векторная диаграмма цепи r и С .
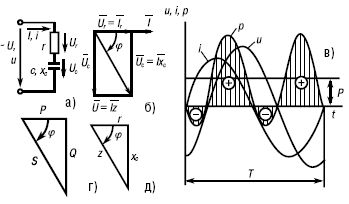
Рис. 16. Электрическая цепь, содержащая резистивный r и емкостный С элементы (а), ее векторная диаграмма (б), графики мгновенных значений (в), треугольники мощностей и сопротивлений (г и д)
Вектор напряжения Ūr совпадает с вектором тока, вектор Ūc отстает от вектора тока на угол 90°. Из диаграммы следует, что модуль напряжения, приложенного к цепи, равен:
![]()
Выразив Ur и Uc через ток и сопротивления, получим: ![]()
откуда ![]()
Последнее выражение представляет собой закон Ома цепи r и C :
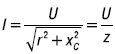
где z – полное сопротивление.
Графики u ( i ), i ( t ) изображены на рисунке 16в. Разделив стороны треугольника напряжений (рис. 16б) на ток, получим треугольник сопротивлений (рис. 16д), из которого можно определить косинус угла сдвига фаз между током и напряжением:
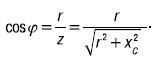
Мгновенная мощность цепи:p = ui = ImsinωtUm × sin (ωt +φ)
Средняя мощность за период: