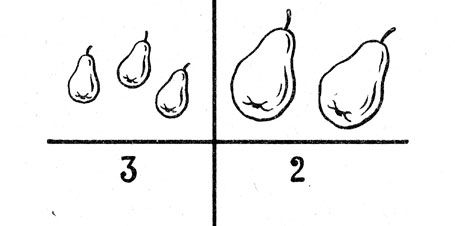
Под рисунками груш написаны цифры
- Что больше - три или два?
- Три больше! - говорят мне дети.
- Значит, где больше груш слева или справа?
- Справа.
- Почему?
И дети мне "объяснили": это же ясно справа большие груши, а слева маленькие.
Только Саша не подчинился тогда феномену Пиаже.
- Неправильно! - сказал он. - Слева три груши, справа - две, значит, слева груш больше!
Я пересек класс и торжественно протянул руку мальчику.
- Дай мне пожать твою руку!
Саша в недоумении протянул мне руку, а класс наблюдал за нами с любопытством: что случилось?
- Спасибо тебе, Саша, что думал! Ты меня очень порадовал!
Вместе с Сашей мы подошли к доске.
- Ребята, смотрите на Сашу, как он будет думать!.. Скажи мне, Саша, где больше кругов - на этой доске или на той? - и я приоткрыл занавески на двух крайних досках, а среднюю закрыл.
На левой доске шесть кругов были нарисованы один в другом, на правой круги были разбросаны по всей площади.

Круги, нарисованные на левой и правой досках
Мальчик внимательно начал разглядывать рисунки на обеих досках.
"Ну, Саша, - думал я про себя, - помоги мне! Сейчас ты можешь сделать гораздо больше для своих одноклассников, чем я! Сейчас ты наилучший учитель для них!"
Я встал посередине класса и в полной тишине начал говорить детям вполголоса:
- Дети, смотрите, как он сосредоточился!.. Видите, он пока ничего не говорит… Не дает сразу волю своему языку, чтобы не ошибиться!
Саша подходит к левой доске и пальцем пересчитывает круги. А я шепчу детям:
- Видите, как он проверяет себя!
И мысленно обращаюсь к Саше: "Не ошибись, Саша, только не сейчас! Нам с тобой очень нужно продемонстрировать всем ребятам, как важно, как необходимо человеку думать и как приятно смотреть на думающего человека! Нам нужно, мальчик, всем классом победить Пиаже! Знаешь, что я читал в одной научной статье? Какой-то ученый развивал мысль, что шестилеток нельзя водить в школу, потому что они, мол, не могут преодолеть феномены Пиаже! Видишь? Конечно, Саша, это не страшно! Шестилетки нашей страны не сегодня-завтра пойдут в школу учиться! Но обидно, когда о них говорят как о неспособных преодолеть эти феномены!"
- На этой доске, - говорит мальчик, указывая на доску, где круги нарисованы один в другом, - кругов больше, 6 кругов, а на той, - указывает на другую доску, - меньше, 5 кругов!
Некоторые дети заспорили с Сашей. "Нет, - считали они, - ну и что же, что там шесть, а там - пять кругов? Все же на правой доске их больше, потому что ими заполнена вся доска. А здесь, видишь, сколько свободного места!"
Но Саша отстаивал свое и нашел в классе единомышленников. "Какая разница, - говорили они, - разбросаны круги или находятся вместе? Шесть всегда будет больше пяти!"…
Так было несколько дней назад. Сегодня я возвращаюсь к "феноменам".
- Поднимите головы! Смотрите и думайте!
Но дети только взглянули на рисунок, и сразу же многие подняли руки.
- Дети, посмотрите на Илико, как он думает! Видите: он не спешит с ответом! Может быть, вы тоже сначала подумаете?
Все опускают руки, оглядываются на Илико, который сосредоточенно смотрит на доску, что-то шепчет про себя и двигает указательным пальцем - пересчитывает квадраты.
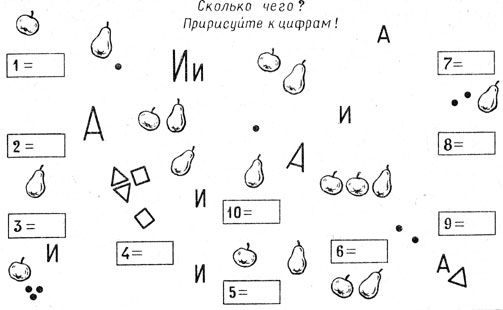
Минута размышления… Дети опять поднимают руки. Наклоняюсь то к одному, то к другому. Уже шесть или восемь ребятишек шепнули мне, что в группе А больше квадратов, чем в группе В. "Нет, - шепчу я каждому, - ответ неправильный!" Но вот Эка мне нашептывает, что в группе А девять квадратов, а в группе В - десять.
- Эка порадовала меня! - говорю я всем. - Спасибо, Эка! - и жму девочке руку.
Ника, Ираклий, Нато, Ия, Гия, Магда отвечают неправильно. "Сосчитайте, пожалуйста, сколько квадратов в каждой группе!"- советую я им. Но Гиге, Сандро, Tee, Майе, Нии, Тенго - каждому в отдельности - я сказал вслух "Спасибо!" и пожал руку.
Да, я говорю детям "Спасибо!", жму им руки, видя, как они думают, находят интересные решения, высказывают и обосновывают свою точку зрения.
Я говорю ребенку "Спасибо!", если он проявляет интерес к знаниям, проблески самостоятельности и вдумчивости, храбрости и упорства. Ведь тем самым он становится моим помощником в своем же воспитании и обучении. Надо поощрять любое старание ребенка, его попытки подняться еще на одну ступеньку своего развития, становления, и я не нахожу лучшего педагогического способа, чем выражать свою радость и благодарность, свое дружеское отношение к нему.
…Итак, что же получается? Значит, мои ребятишки могут преодолеть эти пресловутые феномены Пиаже? Да, видимо, опыт, обучение могут ускорить этот процесс.
- Давайте сосчитаем, сколько квадратов в группе А! предлагаю я детям.
Сосчитали коллективно. Их 9, эту цифру я пишу под рисунком.
Сосчитали квадраты и в группе В. Там 10. Пишу цифру под другим рисунком.
- Где же больше квадратов?
- Конечно, в группе В, - уверяет меня почти весь класс, даже те дети, которые только что шептали мне совсем другое. Но почему же тогда некоторым показалось, что в группе А квадратов больше?
Любопытно, что скажет Магда - почему она ошиблась?
- Квадраты тут разбросаны по всей доске, и потому я подумала, что их здесь больше, чем в группе В.
Ираклий (тоже шептавший мне совсем иное). Не надо смотреть, как они разбросаны, надо сосчитать и так сравнить. Надо думать!
- Верно, всегда надо думать. Я вижу, вам нравятся такие задачи?
- Очень!
- Тогда, кто хочет, пусть подойдет ко мне после уроков, и я дам каждому пакетик с такими задачами!
Захотели получить пакет все. Они два раза брали домой такие заданиями вот уже несколько дней упрашивают меня снова дать им пакетики. В течение всего года я еще много раз буду давать им разные задания в пакетах, каждый раз уточняя: "Кто хочет!", "Если хотите!". Буду предлагать выбирать пакеты со сложными или легкими заданиями. Через день-другой они вернут мне пакетики с решенными задачами, я вместе с ребенком проверю содержимое каждого пакета в свободное от уроков время, а затем положу эти листки с выполненными заданиями в их личные дела, которые я уже завел.
На этот раз в пакетики я вложил карточки со следующими заданиями:
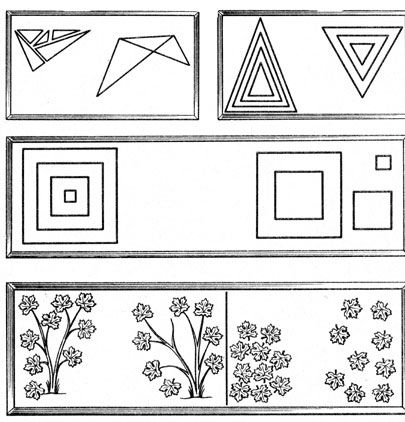
Карточки с заданиями
Карточка с заданиями
Не волнуйтесь, пакет получит каждый, кто пожелает! А теперь откройте ящички с геометрическими фигурами!
- Ура!
На каждой парте для каждого ребенка стоит маленький плоский ящичек из тонкой фанеры (спасибо родителям!). В нем "волшебные" игры. Игры эти, на радость "нулевикам", разработал профессор Б. И. Хачапуридзе. В ящичках лежат пять геометрических фигур круг, треугольник, квадрат, прямоугольник, овал, каждая трех разных величин (большая, средняя, маленькая) и четырех цветов (красная, зеленая, синяя, желтая). (Получается, таким образом, по 12 кружков, 12 треугольников и т. д. Всего же в ящике лежит 60 картонных фигур.)
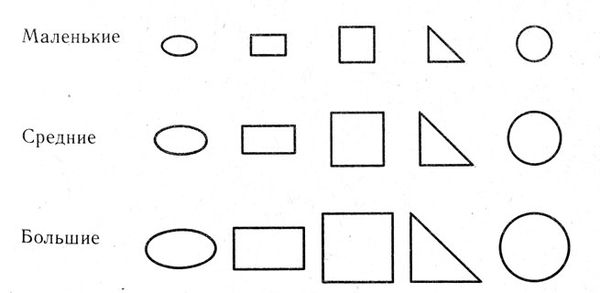
Набор геометрических фигур
Вначале я давал детям простые задания: отобрать только одинаковые фигуры, только большие или маленькие фигуры, только красные, зеленые. Каждый раз дети анализировали фигуры, сгруппированные по тому или иному принципу. Затем я учил ребят группировать фигуры по двум признакам (по величине и цвету), по трем (по форме, величине и цвету), учил находить сходство и различие между ними. Одновременно дети усваивали названия всех этих фигур.
После решения подобных задач предлагал пофантазировать: строить из геометрических фигур разные предметы, например самолеты, космические ракеты, морские суда, автомобили, дома. Я сам вместе с детьми тоже начинал фантазировать: брал демонстрационные (больших размеров) геометрические фигуры и строил "для себя" на доске корабли и автомобили.
Некоторым не нравились мои "выдумки", они находили в них неточности, несоответствия, помогали мне исправлять и улучшать их.
Два дня назад я дал детям более сложное задание.
- Закройте глаза… А теперь представьте, что у вас два прямоугольных треугольника. Какую геометрическую фигуру мы получим, если приставим их друг к другу?
Секунда молчания.
Лали, не открывая глаз, уточнила:
- А треугольники равные?
- Да-да! Спасибо за поправку!
Дети подняли головы и начали шептать мне свои ответы. Обойдя весь класс, я в изумлении спросил детей:
- Как же так? У кого получается опять треугольник, у кого прямоугольник, у кого - квадрат, четырехугольник…
Мы все взяли по два равных треугольника и начали приставлять их друг к другу. Получили три разные фигуры, которые я нарисовал на доске.