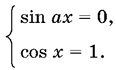
13.29. При решении окажется полезной следующая идея. Если уравнение преобразуется к виду f(x) g(x) = 0, причем корни f(x) находятся легко и содержат все корни g(x), то решать уравнение g(x) не следует. Поскольку в нашем случае уравнение f(x) g(x) = 0 было получено из системы, то остается выяснить, какие из корней уравнения f(x) = 0 приведут к решению исходной системы.
13.30. Первое уравнение можно привести к виду
![]()
При подстановке 2y = /4 − x + kπ приходится рассматривать случаи k = 2p и k = 2p + 1.
13.31. Относительно и и v получится система уравнений, которую удобно решить заменой v = ut.
13.32. С помощью второго уравнения выразить y через x и подставить в первое уравнение системы.
13.33. При решении системы нам придется оба уравнения возводить в квадрат. Следовательно, в конце необходимо сделать проверку.
13.34. Получив из второго уравнения после подстановки в него найденного значения x выражение для |y|, нужно позаботиться о том, чтобы |y| ≥ 0.
13.35. Из третьего уравнения x + y = π − z. Следовательно, tg z = −tg (π − z) = −tg (x + y). (!!)
По формуле тангенса суммы и с помощью уравнения tg y = 2tg x можно выразить tg z через tg x и подставить в первое уравнение.
13.36. Получить уравнения с одинаковыми левыми частями и сравнить их. При решении квадратного уравнения обратить внимание на исследование.
13.37. Прежде чем возводить уравнения в квадрат, оставим в левой части первого уравнения sin x, а в левой части второго уравнения оставим cos x.
13.38. При решении уравнений возникнут арксинусы и арккосинусы, которые будут накладывать ограничения на а. Следует ли к этим ограничениям добавлять |а| ≤ 1, |а + ½| ≤ 1, что вытекает непосредственно из условия?
13.39. Оценив правую и левую части уравнения, обнаружим, что равенство возможно лишь в случае, если обе равны четырем. B результате уравнение сводится к системе. B частности, следует обратить внимание на то обстоятельство, что левая часть равна 4 лишь при tg x = tg y = 1.
13.40. Способ 1. Преобразовать уравнение в сумму квадратов и заменить системой.
Способ 2. Уравнение преобразуется к сумме двух неотрицательных выражений, которая равна нулю. B результате получим систему
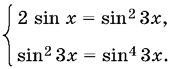
13.41. Способ 1. После преобразования данное уравнение примет вид
![]()
Первые два члена дополнить до полного квадрата и получить сумму неотрицательных слагаемых, которая равна нулю.
Способ 2. Уравнение можно записать в виде
(1 − cos x) cos y + sin x sin y = /2 − cos x
и рассмотреть левую часть как однородное выражение относительно sin y и cos y. Остается оценить выражение A cos y + B sin y и правую часть уравнения.
13.42. Способ 1. Обозначив tg x = z, tg а = с, мы придем к выражению, которое должно быть тождеством относительно x. Остается вспомнить условие тождественного равенства двух многочленов.
Способ 2. Так как равенство
tg x + tg (а − x) + tg x tg (а − x) = b
должно выполняться тождественно, т. е. при всех x, то оно должно быть верным и для конкретных значений x, например при x = 0 и x = /4 . Найденные в результате значения а и b нуждаются в проверке.
13.43. На первый взгляд кажется естественным воспользоваться оценкой
sin² x + /sin² x ≥ 2, cos² x + /cos² x ≥ 2.
Однако это очень грубая оценка. B самом деле, если для одного из выражений достигается равенство, то другое обращается в бесконечность.
Следовательно, нужно преобразовать левую часть уравнения так, чтобы sin² x и cos² x не были разъединены. С этой целью удобно раскрыть скобки и заменить
sinx = ¼ (1 − cos 2x)², cosx = ¼ (1 + cos 2x)².
13.44. Левую часть выражения
sin 2x − sin x cos 2x = /2 ,
к которому приводится данное уравнение, удобно рассмотреть как A sin 2x + B cos 2x, где А = 1, B = -sin x, и оценить.
13.45. Задача сводится к уравнению типа sin α + cos β = 2, которое равносильно системе: sin α = 1, cos β = 1.
13.46. Найдя y из квадратного уравнения, следует использовать и его выражение через x (см. указание I, с. 150). При такой замене появляется опасность приобретения посторонних корней.
13.47. Данную систему уравнений удобно переписать в виде
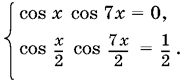
Легко заметить, что следствием полученной системы является уравнение cos 7x = 0, содержащее в качестве корней не только все числа, для которых cos x = 0, но и все корни второго уравнения. B самом деле, при cos 7x = 0 получим cos² /2 = 1 и, следовательно, cos² /2 = ½ . Остается отсеять посторонние значения x.
13.48. Левая и правая части преобразуются к виду, когда в знаменателе и в числителе появляются общие множители. Нужно следить за ограничениями, а в конце провести отбор решений.
13.49. Все ограничения можно объединить: sin 4x ≠ 0. Эти значения нужно исключить из решений уравнения, полученного после преобразований.
13.50. Следить за равносильностью всех преобразований. Отобрать среди корней числителя те, которые не обращают в нуль знаменатель.
13.51. Из полученных значений t нужно отбросить те, для которых sin t = 0, cos t = 0 и cos 2t = 0, а также (это будет видно в процессе преобразований) cos 2t = ½. Первые три ограничения можно объединить: sin 4t ≠ 0.
К главе 14
14.4. Когда мы заменим sin 2x и cos 2x на их выражения через tg x, могут быть потеряны те решения неравенства, при которых sin 2x и cos 2x существуют, а tg x не существует. Однако tg x входит в правую часть данного неравенства, а потому значения x, при которых tg x не существует, не могут быть решениями этого неравенства.
14.5. Способ 1. Чтобы найти секторы круга, в которых tg 2 x ≤ 0, нужно вначале построить радиусы, соответствующие углам, для которых tg 2x = 0 и tg 2x не существует.
Способ 2. B результате применения формулы тангенса двойного угла возможна потеря решений: из области определения выпадают точки, в которых cos x = 0.
14.8. Так как коэффициент при старшем члене положителен, то знаки корней зависят от знака свободного члена.
14.10. Найти те значения k, при которых полученное неравенство осуществимо.
14.11. Воспользоваться тем, что sin x + cos x = √2 cos (x − /4), и решить неравенство относительно y = cos (x − /4).
14.12. Произведение cos x cos 3x, стоящее в знаменателе, выразить через cos 2x. Получится алгебраическое неравенство относительно y = cos 2x.
14.13. При возведении неравенства в квадрат достаточно потребовать, чтобы cos x ≥ 0.
14.15. Обозначить sin α через y и разложить получившийся многочлен третьей степени на множители, воспользовавшись теоремой о делителях свободного члена и первого коэффициента.