9.29. Если каждое из уравнений возвести в квадрат, то получим систему относительно u = x² и v = у². Проверка здесь может оказаться довольно сложной, поэтому целесообразно следить за равносильностью в процессе решения. Чтобы в результате возведения в квадрат не появились посторонние решения, достаточно записать ограничения: x > 0, у > 0.
9.30. Все члены системы, содержащие x и у, однородны второй степени относительно x и у. Пусть данная система имеет решения x1, у1, z1 Укажите симметричное решение, которое наряду с этим будет иметь система.
9.31. Поскольку вместе с условием x + у = 0 мы получаем три уравнения с двумя неизвестными, то имеет смысл воспользоваться подстановкой у = −x.
9.32. Поскольку данная система должна иметь решение при любом b, то, чтобы сузить область допустимых значений а, можно рассмотреть эту систему при некотором фиксированном b.
9.33. Вначале нужно использовать условие, что система должна иметь только одно решение. Второе уравнение можно рассматривать как четную функцию относительно x и у, т. е. наряду с решением x = x1, у = у1 оно имеет три симметричных решения: (−x1, у1), (x1, −у1), (−x1, −у1). Какое из этих решений наряду с (x1, у1) будет удовлетворять первому уравнению?
9.34. Второе уравнение можно преобразовать к виду
![]()
умножив числитель и знаменатель дроби на выражение, сопряженное знаменателю. Легко убедиться, что у ≠ 0. Поэтому можно полученное уравнение разделить на у, после чего нетрудно с помощью первого уравнения системы исключить ![]()
9.35. Представить уравнение в виде
|6 − |x − 3| − |x + 1|| = а(x + 5) + 4,
построить график функции, стоящей в левой части равенства, и рассмотреть поведение относительно этого графика прямой у = а(x + 5) + 4 при разных значениях а.
9.36. Обе части нужно возвести в квадрат. Чтобы обеспечить равносильность, в системе с полученным уравнением придется решать неравенство 4x² − 3аx ≥ 0. При этом выражение под вторым радикалом автоматически будет неотрицательным.
В задачах с параметрами, как правило, нарушать равносильность нецелесообразно. Рассуждения, связанные с ОДЗ, не дают строгого решения.
9.37.x = 0 - корень уравнения. Выражения в знаменателях имеют одинаковую составляющую 5x² + 6.
9.38. Это система однородных уравнений, и она решается стандартной подстановкой x + у = u, xу = v.
K главе 10
10.1. Из условия а + b = 2 следует, что числа а и b расположены симметрично относительно единицы. Использовать этот факт.
10.2. Условие а1а2...аn = 1 можно использовать при преобразовании левой части неравенства, умножая или деля ее на произведение а1а2...аn. Поскольку число множителей 1 + аi совпадает с показателем степени в правой части неравенства и все множители равноправны, то следует доказать, что каждый из них не меньше двух.
10.3. Способ 1. Поделить данное в условии равенство а + b = с почленно на с.
Способ 2. Доказать эквивалентное неравенство:
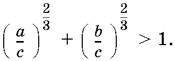
10.4. Избавиться от дробей и использовать условие 0 ≤ x ≤ 1. Это условие обеспечивает выполнение таких неравенств, как x ≤ x, 1 − x ≥ 0 при любом натуральном k. (!)
10.5. Оценить каждый корень с помощью неравенства между средним геометрическим и средним арифметическим двух чисел, взяв в качестве первого числа подкоренное выражение, а в качестве второго единицу.
10.6. Предположить, что b ≤ а, и оценить левую часть данного неравенства, заменив b на а. (!)
10.7. Если бы между правой и левой частями стоял знак равенства, то мы имели бы производную пропорцию от ![]()
10.8. Воспользоваться неравенством между средним арифметическим и средним геометрическим двух чисел.
10.9. Способ 1. Если обозначить три положительных слагаемых в левой части неравенства через u, v и w, то uvw = 1. Следовательно, среди чисел u, v и w есть одно большее единицы и одно меньшее единицы, например, u > 1, v < 1. Тогда (1 − u)(v − 1) > 0.
Способ 2. Если u, v и w - положительные числа, причем w - наименьшее, то u > w, v > w. Неравенство v > w можно умножить на положительное число u − w и полученное неравенство разделить почленно на uw.
Способ 3. Если с < b < а, то можно записать, что b = с + d1, а = b + d2, где d1 и d2 - положительные числа. Подставьте в левую часть неравенства вместо а и b их выражения с + d1 и b + d2- соответственно.
10.10. Преобразования удобно начать с записи S по формуле Герона. Величину S нужно оценить так, чтобы прийти к выражению, симметричному относительно а, b и с. Поскольку из четырех множителей p, p − а, p − b, p − с первый удовлетворяет этому требованию (2р = а + b + с), следует подвергнуть преобразованиям три других множителя. При этом полезно обратить внимание на то обстоятельство, что их сумма равна p:
p − а + p − b + p − с = 3р − (а + b + с) = p.
10.11. Если перемножить крайние и средние скобки, то получатся два трехчлена, отличающиеся только свободным членом. Это позволяет оценить левую часть, выделив квадрат трехчлена, свободный член которого находится посередине между свободными членами первого и второго трехчленов. (!)
10.12. Данные уравнения симметричны относительно у и z и не симметричны (второе) относительно x. Если воспользоваться вторым уравнением и из первого выразить у + z через x, то мы получим простую систему относительно у и z, где x выступает в роли свободного члена.
10.13. Данные уравнения можно переписать в виде
у + z = 5 − x, yz + x(z + y) = 8,
после чего можно получить уравнение, корнями которого будут у и z, а коэффициенты будут зависеть от x.
10.14. Нужно рассмотреть три случая, в зависимости от того, положителен, отрицателен или равен нулю дискриминант трехчлена. Затем обратить внимание на знак старшего коэффициента. (!)
10.15. Так как коэффициент при x² положителен, то ветви параболы направлены вверх. Рассмотреть возможное расположение корней параболы относительно отрезка 1 < x < 2.
10.16. Воспользоваться теоремой Виета и рассмотреть случаи, когда х1 и x2 одного знака и разных знаков.
10.17. Определить направление ветвей параболы и расположение ее корней относительно точек −1 и +1, чтобы условия задачи выполнялись.
10.18. Если m ≠ 0 (случай m = 0 следует рассмотреть отдельно), то ветви параболы у = mx² − 4x + 3m + 1 должны быть направлены вверх.