Глава 19
Последовательности и прогрессии
Рассмотрим функцию натурального аргумента аn = f(n), где либо n = 1, 2, 3, ..., k, либо n = 1, 2, 3, ..., k, ... . Если при любых натуральных i и j, таких, что i < j, значение аj считается последующим по отношению к аi, то множество значений аn этой функции образует последовательность.
Последовательность обозначают, записывая ее члены аn один за другим в порядке возрастания номера n: а1, a2, а3, ... .
Если номер n принимает значения n = 1, 2, 3, ..., k, то последовательность называется конечной. Если же n = 1, 2, 3, ... (т. е. n пробегает все натуральные числа), то последовательность называется бесконечной.
аn = f(n) называется общим членом последовательности. Если для любых i и j, таких, что i < j, выполняется неравенство аi < аj, то последовательность называется возрастающей. Если при тех же условиях будет аi > аj, то последовательность называется убывающей. Если же при любых i и j, таких, что i < j, выполняется неравенство аi ≤ аj (аi ≥ аj), то последовательность называется неубывающей (невозрастающей).
Последовательность, в которой
аi + 1 = аi + d
при всех натуральных i, называется арифметической прогрессией. Число d называется разностью арифметической прогрессии. Имеют место формулы:
2аn = аn + 1 + аn − 1; аn = а1 + d(n − 1);
где Sn - сумма n первых членов прогрессии.
Последовательность, в которой
ai + 1 = qai
при всех натуральных i, причем q ≠ 0 и ai ≠ 0, называется геометрической прогрессией, а число q называется ее знаменателем.
Для геометрической прогрессии имеют место формулы:
an = a1q ;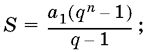 
a²n = an − 1an + 1.
Вторая формула верна, если q ≠ 1. Бесконечная геометрическая прогрессия, у которой |q| < 1, называется бесконечно убывающей.
Бесконечно убывающая геометрическая прогрессия не обязательно является убывающей последовательностью. Она может быть возрастающей, например, при a1 = −1, q = ½ , а может быть колеблющейся: a1 = 1, q = −½ .
Если для бесконечной последовательности существует конечный предел последовательности ее сумм Sn, т. е. существует 
, то S называется суммой всех членов этой бесконечной последовательности.
Для того чтобы бесконечная геометрическая прогрессия имела сумму всех своих членов, необходимо и достаточно, чтобы она была бесконечно убывающей. В этом случае
19.1. Общий член последовательности 
Является эта последовательность возрастающей или убывающей?
19.2. Докажите, что если члены ap, aq, ar, as арифметической прогрессии образуют геометрическую прогрессию, то последовательность p − q, q − r, r − s является геометрической прогрессией.
19.3. Докажите, что если положительные числа a, b, с - соответственно m-й, n-й и p-й члены как арифметической, так и геометрической прогрессии, то
a b с = 1.
19.4. Докажите, что если а, b, с образуют геометрическую прогрессию, то
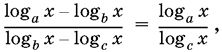
где x > 0, x ≠ 1, а, b, с - различные положительные числа, отличные от единицы.
19.5. Найдите сумму
S = 7 + 77 + 777 + ... + 777...7,
где последнее слагаемое содержит n цифр.
19.6. Докажите, что 
где цифра 1 повторяется 2n раз, и цифры 2 и 3 только n раз.
19.7. При каких значениях x и у последовательность а1, а2, а3, где