Глава 14
Тригонометрические неравенства
Решите неравенства:
14.1. |sin x| > |cos x|.
14.2. 1 − sin x + cos x < 0.
14.3. sin x − З cos x < 0.
14.4. 2 cos 2х + sin 2х > tg x.
14.5. cos x tg 2х ≤ 0.
14.6. 6 + cos 2х + 13 cos x ≥ |5 − 2 cos 2х − 6 sin² x − З cos x|.
14.7. Найдите решения неравенства
sin 2х > √2 sin² x + (2 − √2) cos² x,
лежащие в интервале (0, 2π).
14.8. При каких значениях α, 0 ≤ α ≤ π, уравнение
2х² − 2(2 cos α − 1)x + 2 cos² α − 5 cos α + 2 = 0 имеет различные действительные корни? Исследуйте знаки корней.
Решите неравенства:
14.9.![]()
14.10.![]()
14.11. 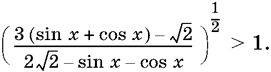
14.12. tg x tg 3x < −1.
14.13.![]()
14.14. Найдите все значения x из интервала 0 < x < π, удовлетворяющие неравенству
![]()
14.15. Докажите, что при любом а имеет место неравенство
4 sin 3α + 5 ≥ 4 cos 2α + 5 sin α.
14.16. Решите неравенство
a² sin² x ≤ sin² 3x, а > 0.
14.17. При каких значениях x и у выражение
(2 cos t + ½ cos x cos у ) cos x cos у + 1 + cos x − cos у + cos 2t
положительно при всех значениях t? Укажите, где на координатной плоскости расположены точки (x, у), удовлетворяющие этому условию.
Глава 15
Трансцендентные неравенства
Решите неравенства:
15.1. (logsin x 2)² < logsin x (4 sin³ x).
15.2. ![]()
15.3. Найдите решения неравенства
log2 cos x > log2 tg x,
удовлетворяющие условию 0 ≤ x ≤ π.
Решите неравенства:
15.4. 4 log16 cos 2х + 2 log4 sin x + log2 cos x + 3 < 0.
15.5. log|cos x + √3 sin x|½ > 0, если 0 ≤ x ≤ 2π.
15.6. sin |lg x| + cos |lg x| > − /√2.
15.7.![]()
15.8. arctg √x > arccos (1 − x).
15.9. (4х − x² − 3) log2 (cos² πх + 1) ≥ 1.
15.10.![]()
Глава 16
Трансцендентные уравнения
16.1. Докажите, что уравнение
2 sin² /2 sin² /6 = /x² + x²
не имеет корней.
Решите уравнения:
16.2.![]()
16.3. (tg x) = (ctg x).
16.4. sin (2 + 2) cos (2 + 2) = ¼.
16.5. lg sin x + lg sin 5х = lg sec 4х.
16.6. lg² (sin x + 4) + 2 lg (sin x + 4) − /4 = 0.
16.7. logsin x (sin x − ¼ cos x) = 3.
16.8. log8 cos² x sin x = ½.
16.9. Найдите положительные решения уравнения
tg [ 5π(½)] = 1.
16.10. Решите уравнение
lg² cos x + 2 lg cos x + m² + 2m − 3 = 0.
16.11. Для каждого действительного числа а решите уравнение
lg² sin x − 2а lg sin x − а² + 2 = 0.
16.12. Решите систему уравнений
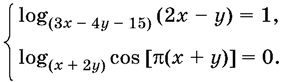
16.13. Решите уравнение
4 + 4 = −8x² + 12|x| − ½.
16.14. Решите уравнение
![]()
Глава 17
Функции и их свойства
17.1. Решите неравенство
4f(x) + g(x) ≤ 0,
если функции f(x) и g(x) удовлетворяют системе
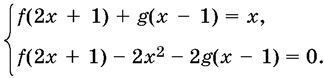
17.2. Сколько различных действительных корней имеет уравнение f(f(x)) = 0, где f(x) = x³ − 6x² + 9x?
17.3. Найдите все целые x и у, удовлетворяющие системе
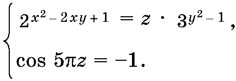
17.4. Решите систему уравнений
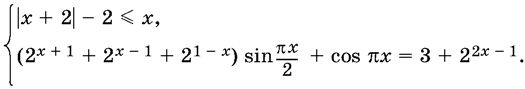
17.5. Дана функция f(x) = 6х² + 2х + 6. Известно, что ее график касается графика первообразной F(x) этой функции в точке, абсцисса которой превосходит число 0,7. Найдите все значения x, для которых
![]()
17.6. Изобразите на плоскости (x, у) множество точек, координаты которых удовлетворяют неравенству
log(x − у)(x + у) ≥ 1.
17.7. Найдите площадь фигуры, координаты точек которой удовлетворяют системе неравенств
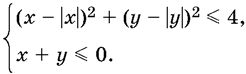
17.8. На координатной плоскости заданы точки A(0; 2), B(1; 7), С(10; 7) и D(7; 1). Найдите площадь пятиугольника ABCDE, где E - точка пересечения прямых AC и BD.
17.9. Фигура задана на координатной плоскости системой