Равенство, в котором правая и левая части являются тождественными выражениями, называется тождеством.
Для обозначения тождественного равенства иногда используется символ ≡.
Примеры тождеств: (а − b)² = а² − 2аb + b², sin² x + cos² x = 1,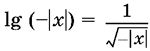 
Первые два тождества общеизвестны. Последнее равенство тоже является тождеством. В самом деле, область определения левой части не содержит ни одной точки, область определения правой части тоже не содержит ни одной точки. Поскольку области определения правой и левой частей - пустые множества, то требования 1) и 2) в определении тождества удовлетворяются. Равенство 
, как мы видели, истинно при всех x, кроме x = −1. Оно не является тождеством, так как требование 1) не удовлетворено. Однако нарушение происходит только в одной точке.
Введем понятие неабсолютного тождества.
Пусть в нашем распоряжении есть два математических выражения, имеющих разные области определения. Обозначим через U их общую часть. Если на множестве U значения обоих математических выражений совпадают, то говорят, что они неабсолютно тождественны, а соответствующее равенство называют неабсолютным тождеством.
Характерным примером неабсолютного тождества является соотношение
lg ху = lg x + lg у.
Область определения правой части: x > 0, у > 0, т. е. все точки плоскости, лежащие внутри I квадранта. Область определения левой части: x > 0, у > 0; x < 0, у < 0; это уже будут внутренние точки I и III квадрантов. Общая часть областей определения: x > 0, у > 0. На этой общей части приведенное соотношение превращается в истинное равенство.
Напомним определение тождества, которым обычно пользуются в средней школе.
Тождеством называется равенство, справедливое при всех значениях входящих в него букв, при которых обе его части имеют смысл.
Нетрудно заметить, что это определение объединяет понятия тождества и неабсолютного тождества в одно. Чтобы подчеркнуть, что мы пользуемся другим определением тождества, будем иногда вместо термина тождество употреблять термин абсолютное тождество.
Упражнения
Какие из следующих равенств являются абсолютными тождествами, а какие - неабсолютными? Приведите доказательство сделанного вами вывода.
1. sin² x + cos² x = 1,
2. tg x = /cos x
3. tg x = /ctg x
4. sec x = /cos x
5. sec x cos x = 1,
6. sec x − /cos x = 0,
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. lg xy = lg |x| + lg |y|,
15. lg x² = 2 lg x,
16. lg x² = 2 lg |x|.
Уравнение, корни уравнения, равносильность. Когда мы говорим, что равенство
аx² + bx + с = 0 (1)
является уравнением относительно буквы x, то подразумеваем, что для фиксированных а, b и с (эти буквы являются параметрами уравнения) нужно отыскать значения x, обращающие (1) в истинное числовое равенство.
Другими словами, предполагают, что для букв а, b и с выбраны определенные, хотя и произвольные, значения, в то время как буква x, которой обозначено неизвестное, остается "свободной". Вместо нее можно подставлять различные числа, в результате чего возникнут либо истинные, либо ложные числовые равенства. Равенство (1) выполняет роль "формы" (или "схемы") уравнений, которая превращается в уравнение, как только мы остановим свой выбор на конкретных значениях параметров. Если выбор значений параметров уже сделан, то полученное уравнение можно рассматривать как "форму" числовых равенств - ложных или истинных.
Часто представляют себе уравнение как равенство двух функций (в частности, как равенство функции нулю), а не как форму. Такое представление недостаточно точно, так как может привести к потере корней.
Например, уравнение
x = 1 (2)
имеет корни x1 = 1 и x2 = −1, в то время как функция x определена только при положительных x.
Если же уравнение (2) мы рассматриваем как форму, порождающую числовые равенства, то при x = −1 слева получим выражение (−1), которое имеет смысл и равно 1.
Итак, уравнением относительно неизвестного x называется форма числовых равенств, которая превращается в истинное или ложное числовое равенство при подстановке вместо буквы x какого-нибудь числа, взятого из рассматриваемой области чисел. Приведем еще несколько определений.
Пусть x, у, z, ... - неизвестные в уравнении
f(x, у, z, ...) = 0. (3)
Набор значений неизвестных
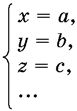
называется решением уравнения (3), если
f(а, b, с, ...) = 0 (3′)
является истинным числовым равенством.
Решение уравнения с одним неизвестным называют также корнем этого уравнения.
Корнем уравнения 3x² + 2x − 1 = 0 является число x = −1, решением уравнения 2у² − 3xу + x² = 0 является система чисел