Рене Декарт в детстве отличался хрупким здоровьем, но был чрезвычайно любознательным. Начальное образование он получил в иезуитском колледже. Учителя отбили, казалось, его природное стремление к познанию. Некоторое время он вел разгульный образ жизни, играл в карты. Однако религиозное образование сыграло и свою положительную роль в становлении ученого. Оно только укрепило в молодом Декарте недоверие к тогдашней философии и настроило на поиск своих ответов на вопросы, которые он сам для себя определял. Позже Декарт сформулировал свой метод познания как дедуктивные (математические) рассуждения над результатами воспроизводимых опытов. Достаточно времени было отдано Декартом военной службе, на которую он поступил, чтобы больше и не понаслышке узнать мир. Сначала он был в революционной Голландии, затем в Германии, где участвовал в недолгой битве за Прагу (Тридцатилетняя война). Затем – еще участие в осаде Ла-Рошели. Все это время он продолжал заниматься философией и математикой, как ее частью, и другими науками – от медицины до метеорологии. Он вел обширную переписку с лучшими учеными Европы. Свободомыслие Декарта стало известно иезуитам, и те обвинили его в ереси. Поэтому Декарт в 1628 году переезжает в Голландию, где проводит 20 лет. В 1634 году он закончил свою первую, очень важную книгу под названием "Мир". Но момент для издания был неудачным – годом ранее инквизиция судила Галилея. Теория Коперника, принятая и в книге Декарта, была официально запрещена. Поэтому Декарт решил не печатать этот труд.
Известная всем "Геометрия" Декарта была опубликована в 1637 году. Вряд ли он испытывал влияние Ферма, его метод сложился задолго до выхода "Геометрии", еще в 1620-х годах. Тем не менее собственно геометрические идеи Декарта и Ферма практически тождественны. Заслуга Декарта в том, что он создал новую алгебру, основанную на понятии отношения геометрических величин. Ферма был подвержен влиянию геометрической алгебры греков. У него и математиков, которым он следовал, можно складывать и вычитать только однородные величины, а в коэффициенты обязательно включается указание на их геометрическую природу. При этом простое алгебраическое уравнение раздувается неимоверно. Декарт, прежде всего, был философом, основоположником рационализма, утверждающего неограниченную способность человека познавать мир. Отношения, с которыми имеет дело алгебра Декарта, не геометрические пространственные объекты, а умозрительные понятия – "числа", мало того, выраженные "буквами". Его символика мало чем отличается от современной. Он следует некоторому набору интуитивно ясных истин и использует определенные правила или методы.
Именно Декарт впервые ввел координатную систему, которая является прообразом принятой в наши дни, но идеологически несколько отличается. Он далеко не всегда использовал прямоугольную систему координат. Кривая на плоскости рассматривалась относительно некоторой прямой с делениями. Положение точек кривой задавалось с помощью системы параллельных отрезков, перпендикулярных или наклонных к исходной прямой. Декарт не вводил второй координатной оси, не фиксировал направление отсчета от начала координат. Современное представление координатной системы, получившее имя Декарта, сформировалось только в XVIII веке. В ней для каждой из координат обычно вводят взаимно перпендикулярные оси, расстояния на которых градуированы одинаково. Тогда, например, легко вычисляется длина радиус-вектора в трехмерном пространстве (рис. 4.1):
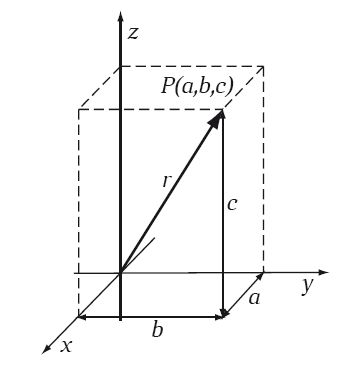
Рис. 4.1. Система координат Декарта
r = x + y + z = a + b + c.
В итоге, появилось ясное понимание, как определить положение тела (точки) как на плоскости, так и в 3-мерном пространстве.
Абсолютные пространство и время
Итак, мы отметили два ключевых понятия: протяженность и длительность. Возникает вопрос: по отношению к чему производить их измерение? Один из ответов, кажущийся наиболее естественным, состоит в признании существования абсолютного пространства и времени. Тогда и протяженность, и длительность, и абсолютные пространство и время приобретают самостоятельный физический смысл, становятся частью всего физического учения.
Как определял "абсолютное" пространство Ньютон? Он говорил: "Абсолютное пространство по самой своей сущности, безотносительно к чему бы то ни было внешнему, остается всегда одинаковым и неподвижным".
Поскольку гелиоцентрическая система стала общепризнанной, то в качестве абсолютного он определял пространство, привязанное к центру тяжести Солнечной системы. Абсолютное пространство представлялось фоном для всей Вселенной, являлось состоянием абсолютного покоя. По отношению к нему в принципе можно определить абсолютное движение тела – от одной абсолютно покоящейся точки к другой.
Аналогично абсолютному пространству, Ньютон постулировал существование абсолютного времени. Он писал в своих "Началах": "Абсолютное частное математическое время само по себе и по своей сущности, без всякого отношения к чему-либо внешнему, протекает равномерно и иначе называется длительностью". Другими словами, время идет с неизменной скоростью от одного абсолютного момента к следующему, независимо от того что происходит во Вселенной. Или – для любого наблюдателя, находящегося в любом состоянии движения и в любой точке пространства, время представляется ровным, непрерывным, одинаковым (одним и тем же) потоком, определяющим смену событий.
Инерциальная система отсчета. Принцип относительности Галилея
Если в рамках точности измерений времени той эпохи можно было согласиться, что часы с одними и теми же (лучшими) техническими характеристиками идут одинаково у всех возможных наблюдателей, а время, измеренное ими, можно считать абсолютным, то с измерениями абсолютных положений ситуация требовала осмысления. Если принципиально возможно определить координаты (положение) какой-либо точки относительно системы, связанной с центром тяжести Солнечной системы, то осуществить это практически на обращающейся вокруг Солнца Земле сложно.
Чтобы разобраться с ситуацией, необходимо ввести несколько определений. Под системой отсчета обычно понимают строго заданный способ измерения положения и времени. Такие измерения можно осуществлять с помощью системы декартовых координат (трех взаимно перпендикулярных осей) – для измерения положения и расстояний и с помощью часов – для отсчета времени. Инерциальной системой называется система отсчета, в которой тела при отсутствии внешних воздействий движутся равномерно и прямолинейно, то есть система, в которой работает первый закон Ньютона. Тогда, как минимум, абсолютное пространство вместе с абсолютным временем может мыслиться как инерциальная система отсчета.
Возникает вопрос: есть ли еще инерциальные системы и как они относятся к абсолютному пространству? Обратимся к так называемым преобразованиям Галилея (термин был введен в 1909 году). Они определяют связь между координатами для двух систем отсчета, движущихся относительно друг друга. Если скорость V направлена вдоль оси x, то координаты x в двух системах для постоянной скорости связаны соотношением: x′ = x + Vt. Время t, определенное в механике Ньютона как абсолютное, является одинаковым для всех систем отсчета. Для преобразований Галилея скорость движения частицы v′ в одной системе определяется как простая сумма скорости этой частицы в другой системе и скорости относительного движения систем V, если скорость частицы и относительная скорость систем имеют одно направление: v′ = v + V. Например, если в поезде выстрелят в направлении его движения, то для наблюдателя на перроне скорость пули будет определяться как сумма скорости поезда и скорости пули относительно оружия. Если скорости не параллельны, то используется векторная сумма. Таким образом, преобразования Галилея ясно показывают, что любая система отсчета, движущаяся равномерно и прямолинейно относительно какой-либо инерциальной системы (скажем, абсолютного пространства), также является инерциальной. Это и есть ответ на вопрос.
Возвратимся к измерениям на Земле. Обычно они производятся в ограниченном пространстве (малом, по сравнению с размерами Земли) и ограничены во времени – малые длительности по сравнению с периодом обращения вокруг Солнца (годом). Такая "лаборатория" с большой степенью точности движется равномерно и прямолинейно относительно абсолютного (по Ньютону) пространства. Если с ней связаны пространственные и временные координатные системы, то она будет инерциальной системой отсчета.