Всего за 114.9 руб. Купить полную версию
![]()
(Естественно, предполагаем, что все пары соседних элементов входят в множество К ). Естественно сравнение проводить с помощью описывающих результаты экономической деятельности функций, участвующих в задачах (1) и (2). Именно, будем говорить, что план Х 1 лучше плана Х 2 при реализации с момента i , если
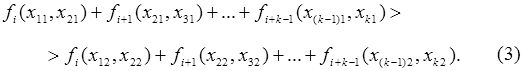
Будем писать Х 1 R(i)Х 2 , если выполнено неравенство (3), где R(i) – бинарное отношение на множестве планов, задающее упорядочение планов отношением "лучше".
Ясно, что упорядоченность планов на k шагов, определяемая с помощью бинарного отношения R(i), может зависеть от i , т. е. "хорошесть" плана зависит от того, с какого момента i он начинает осуществляться. С точки зрения реальной экономики это вполне понятно. Например, планы действий, вполне рациональные для периода стабильного развития, никуда не годятся в период гиперинфляции. И наоборот, приемлемые в период гиперинфляции операции не принесут эффекта в стабильной обстановке.
Однако, как легко видеть, в моделях с дисконтированием (2) все упорядочения R(i) совпадают , i = 1,2, …, m-k. Оказывается – это и есть основной теоретический результат настоящего подпункта – верно и обратное: если упорядочения совпадают, то мы имеем дело с задачей (2) – с задачей с дисконтированием, причем достаточно совпадения только при k =1,2. Сформулируем более подробно предположения об устойчивости упорядочения планов.
(I). Пусть
![]()
Верно одно из двух: либо
![]()
для всех
![]()
либо
![]()
для всех
![]()
(II). Пусть
![]()
Верно одно из двух: либо
![]()
для всех
![]()
либо
![]()
для всех
![]()
Как впервые подробно показано в работе [4], при некоторых внутриматематических условиях регулярности из условий устойчивости упорядоченности планов (I) и (II) следует существование констант
![]()
и
![]()
таких, что
![]()
Поскольку прибавление константы не меняет точки, в которой функция достигает максимума, то последнее соотношение означает, что условия устойчивости упорядоченности планов (I) и (II) характеризуют (другими словами, однозначно выделяют) модели с дисконтированием среди всех моделей динамического программирования.
Математические условия, при которых доказывалась теорема о характеризации моделей с дисконтированием, постепенно ослаблялись на протяжении 1970–х годов, однако на экономическую сторону дела эти внутриматематические усовершенствования не влияли.
Асимптотически оптимальные планы. Рассмотрим модель (2) с
![]()
т. е. модель без дисконтирования
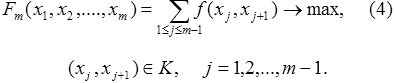
При естественных математических предположениях, на которых не будем останавливаться, при каждом m существует оптимальный план
![]()
при котором достигает максимума оптимизируемая функция. Поскольку выбор горизонта планирования нельзя рационально обосновать, хотелось бы построить план действий, близкий к оптимальному при различных горизонтах планирования. Это значит, что целью является построение бесконечной последовательности
![]()
такой, что ее начальный отрезок длины m, т. е.
![]()
, дает примерно такое же значение оптимизируемого функционала, как и значение для оптимального плана
![]()
Бесконечную последовательность
![]()
назовем асимптотически оптимальным планом.
Выясним, можно ли использовать для построения асимптотически оптимального плана непосредственно оптимальный план. Зафиксируем k и рассмотрим последовательность
![]()
Нетрудно построить примеры, показывающие, что, во-первых, элементы в этой последовательности будут меняться; во-вторых, они могут не иметь пределов. Следовательно, оптимальные планы могут вести себя крайне нерегулярно, а потому в таких случаях их нельзя использовать для построения асимптотически оптимальных планов.
Тем не менее можно доказать, что асимптотически оптимальные планы существуют, т. е. можно указать такие бесконечные последовательности
![]()
, что