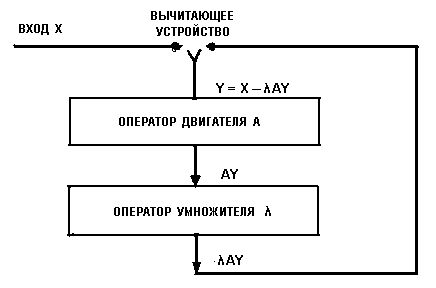
Рис. 2
Здесь входной сигнал двигателя, обозначенный через Y, равен разности между первоначальным входным сигналом Х и выходным сигналом умножителя, умножающего выходную мощность AY двигателя на коэффициент λ. Тогда
(4.18)
и
, (4.19)
откуда выходной сигнал двигателя
. (4.20)
Следовательно, оператор, создаваемый всем механизмом обратной связи, равен A/(1+ λA). Он будет бесконечно большим тогда и только тогда, когда А= -1/λ. Кривая (4.17) для этого нового оператора будет иметь вид[c.170]
, (4.21)
и ∞ будет внутренней точкой этой кривой тогда и только тогда, когда -1/λ является внутренней точкой первоначальной кривой (4.17).
В этом случае обратная связь с коэффициентом λ, несомненно, произведет нечто катастрофическое, и эта катастрофа практически выразится в том, что система придет в неограниченные, нарастающие колебания. Если же точка -1/λ внешняя, то можно показать, что никаких неприятностей не будет, и обратная связь будет устойчивой. Случай, когда точка -1/λ лежит на эффективной границе, требует особого исследования. В большинстве случаев система может прийти при этом в колебание с амплитудой, которая не будет увеличиваться.
Пожалуй, полезно рассмотреть несколько операторов А и допустимые для них диапазоны обратной связи. Мы будем рассматривать не только операции (4.02), но и их пределы, предполагая, что к последним применимы те же рассуждения.
Если оператор А соответствует дифференциальному оператору, то A(z)=z; тогда при изменении y от -∞ до ∞ точно так же изменяется и А (y), и внутренние точки являются внутренними точками правой полуплоскости. Точка -1/λ всегда является внешней, и любая степень обратной связи возможна.
Если
, (4.22)
то кривая (4.17) принимает следующий вид:
, (4.23)
или
, 
, (4.24)
что можно также записать в виде
(4.25)
[c.171]
Таким образом, наша кривая есть окружность с радиусом 1/2 и центром в точке (1/2, 0). Обход ее совершается по часовой стрелке, и внутренними будут те точки, которые обычно считаются внутренними. В этом случае обратная связь также неограниченна, ибо точка -1/λ всегда находится вне круга. Оператор a(t), соответствующий этому оператору А, будет равен
. (4.26)
Положим теперь
, (4.27)
тогда (4.17) принимает вид
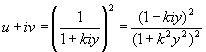(4.28)
Или
, 
(4.29)
что дает
(4.30)
или
(4.31)
Тогда
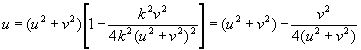(4.32)
В полярных координатах при u = ρ соs φ, v = ρ sin φ получим
(4.33)
или
(4.34)
Иными словами, [c.172]
(4.35)
Можно показать, что оба эти уравнения изображают одну кривую - кардиоиду с вершиной в начале координат и острием, направленным вправо. Внутренняя область этой кривой не содержит точек отрицательной действительной оси; как и в предыдущем случае, допустимое усиление неограниченно. Оператор а(t) для этого случая имеет следующий вид:
(4.36)
Положим еще
(4.37)
Определим ρ и φ, как в предыдущем случае. Тогда
(4.38)
Как в первом случае, отсюда получим
(4.39)
т. е.
(4.40)
Эта кривая имеет форму, показанную на рис. 3. Заштрихованная область изображает внутренние точки. Коэффициент обратной связи не может быть больше 1/8. Соответствующий оператор a(t) равен
(4.41)