Обратим внимание на то существенное обстоятельство, что в этом выражении интегрирование производится от 0 до ∞, а не от -∞ до ∞. В противном случае мы могли бы с помощью различных практических устройств преобразовать наш сигнал в f(t+σ), где σ положительно. Но это предполагает знание будущего функции f(t), a f(t) может быть величиной, которая не определяется однозначно своим прошлым; пример - координаты трамвая, который может повернуть на стрелке в ту или другую сторону. Если физический процесс по видимости дает нам оператор, преобразующий f(t) в
(4.03)
[c.166]
где а(τ) не исчезает при отрицательных τ, это значит, что мы не имеем больше истинного оператора для f(t), определяемого однозначно прошлым этой функции. Такое может встретиться в реальных физических ситуациях. Например, динамическая система без входа может прийти в постоянные колебания или даже в колебания, нарастающие до бесконечности, с неопределенной амплитудой. В этом случае будущее системы не определяется ее прошлым, и мы, наверное, можем найти формализм, в котором бы использовался оператор, зависящий от будущего.
Операция, посредством которой получено выражение (4.02) из f(t), имеет еще два существенных свойства: 1) она не зависит от сдвига начального момента и 2) она линейна. Первое свойство выражается утверждением, что если
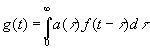, (4.04)
то
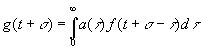. (4.05)
Второе выражается утверждением, что если
, (4.06)
то
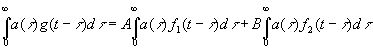. (4.07)
Можно показать, что в некотором подходящем смысле всякий оператор для прошлого функции f(t), линейный и инвариантный относительно сдвига начального момента, имеет вид (4.02) или является пределом последовательности операторов этого вида. Например, f’(t) есть результат применения оператора с такими свойствами к f(t), и потому [c.167]
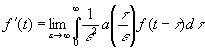, (4.08)
где
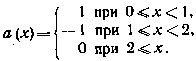(4.09)
Как мы уже видели, функции е составляют особенно интересное семейство с точки зрения оператора (4.02), поскольку
, (4.10)
и оператор задержки становится просто множителем, зависящим от z. Оператор (4.02) переходит тогда в
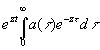. (4.11)
и также оказывается оператором умножения, зависящим только от z. Выражение
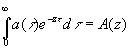(4.12)
называется представлением оператора (4.02) в виде функции частоты. Если z - комплексная величина х+iy, где х и y - действительные числа, то (4.12) переходит в
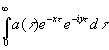(4.13)
Отсюда следует ввиду известного неравенства Шварца для интегралов, что если y>0 и
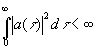, (4.14)
то [c.168]
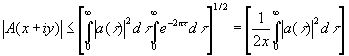. (4.15)
Это значит, что А(х+iу) - ограниченная голоморфная функция комплексной переменной в каждой полуплоскости x≥ε>0, а функция A(iy) представляет в некотором весьма определенном смысле граничные значения этой функции.
Положим
, (4.16)
где u и v - действительные числа. Тогда x+iy определится как функция (не обязательно однозначная) от u+iv. Это функция аналитическая, хотя и мероморфная, за исключением точек u+iv, соответствующих точкам z=x+-iy, где ∂А(z)/∂z=0. Граница х=0 перейдет в кривую с параметрическим уравнением
(y действительное). (4.17)
Эта новая кривая может пересекать саму себя любое число раз, но в общем случае она будет делить плоскость на две области. Рассмотрим кривую (4.17), вычерченную в направлении возрастания y от -∞ до +∞. Если идти от нее вправо по непрерывной линии, не пересекающей снова кривую (4.17), можно попасть в те или иные точки плоскости. Точки, не входящие в это множество и не лежащие на кривой (4.17), мы будем называть внешними точками. Часть кривой (4.17), содержащую предельные точки внешних точек, назовем эффективной границей. Все остальные точки будут именоваться внутренними точками. На нашем чертеже с границами, проведенными в направлении стрелок (рис. 1), внутренние точки заштрихованы, а эффективная граница выделена жирной линией.
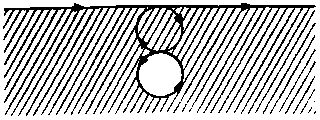
Рис. 1
[c.169]
Условие ограниченности функции А в любой правой полуплоскости указывает на то, что бесконечно удаленная точка не может быть внутренней точкой. Она может быть граничной точкой, хотя существуют весьма определенные ограничения на тип граничной точки, которой может быть бесконечно удаленная точка. Эти ограничения касаются "толщины" множества внутренних точек, простирающихся к бесконечности.
Мы переходим теперь к математической формулировке задачи о линейной обратной связи. Пусть структурная (не электрическая!) схема нашей системы имеет вид, как на рис. 2.