К причинно-регрессионным моделям относятся методы простого и множественного регрессионного анализа. Например, простая линейная регрессия определяется как линейный тренд. Для его расчета может быть применен метод наименьших квадратов, который заключается в подборе прямой линии так, чтобы разброс имеющихся значений показателя по обе стороны от нее был наименьшим. Минимизируется сумма квадратов вертикальных расстояний между линией и каждым фактическим наблюдением (6-1):
у = a + b • х, (6-1)
где у – расчетное прогнозируемое значение показателя (зависимая переменная);
x – факторный признак, определяющий прогнозируемое значение показателя (независимая переменная);
a – отрезок, отсекаемый прямой на оси ординат (определяется по формуле (6-2));
b – коэффициент регрессии (определяется по формуле (6-3)).
а = yср – b • xср, (6-2)
где yср – среднее значение у; xср – среднее значение х.
![]()
где n – количество имеющихся фактических данных или наблюдений.
Для расчета коэффициентов а и b можно воспользоваться программой MS Excel (Сервис ? Анализ данных ? Регрессия).
Спрос, как правило, зависит от нескольких факторов, которые могут быть учтены при помощи метода множественного линейного анализа, когда в уравнении регрессии фигурирует более чем одна независимая переменная. Ниже представлено многофакторное уравнение множественной регрессии:
у = а + b1 • х1 + b2 • х2 + ... + bm • хm , (6-4)
где m – количество независимых переменных (факторных признаков).
Одной из проблем, которая может возникнуть при использовании метода регрессионного анализа, является необходимость определения значений независимых переменных. Для целого ряда факторов это представляет определенную сложность, особенно для факторов макро– и мезоуровней. Кроме того, важным условием адекватного применения регрессионных методов является относительная стабильность среды функционирования сервисной организации. Однако могут появиться новые значимые факторы, измениться характер воздействия существующих и т. п. В такой ситуации между спросом и факторами, его определяющими, возможно, установится совсем другая зависимость по сравнению с прогнозируемой.
Другой группой количественных методов прогнозирования являются методы анализа временных рядов, которые также имеют ограниченную область применения.
Временной ряд состоит из последовательности равномерно распределенных во времени (с интервалом в сутки, неделю, месяц и т. д.) статистических данных по прогнозируемому показателю.
Основная предпосылка при прогнозировании с помощью временных рядов состоит в том, что будущее значение прогнозируемого показателя находится в зависимости только от его прошлых значений, а другие факторы, кроме фактора времени, во внимание не принимаются. Поэтому использование этой группы методов оправдано лишь в условиях сохранения существующих тенденций изменения прогнозируемого показателя и отсутствия влияния новых факторов или изменения действующих.
К методам прогнозирования с помощью временных рядов относятся следующие: "наивный" метод; скользящие средние и его модификации – метод взвешенной скользящей средней и экспоненциальное сглаживание; экстраполяция; прогнозирование на основе сезонных колебаний (см., например: [Стивенсон, 1998; Хаксевер, Рендер, Рассел, Мердик, 2002; Эддоус, Стэнсфилд, 1997; Fitzsimmons J., Fitzsimmons М., 2006]).
"Наивный" метод основывается на предположении, что спрос в следующий период будет равен спросу в последний период времени. Если для данных временного ряда характерны сезонность или тренд, то прогнозируемое значение рассчитывается с учетом соответствующей поправки. Этот метод практически не требует каких-либо затрат, для него характерны быстрота и простота реализации, однако точность его невысока.
Метод скользящих средних предполагает расчет прогнозного значения на основе усреднения нескольких последних показателей. По мере поступления новых данных значения средних обновляются, как показано в формуле (6-5):
Ft+1 = (Dt + Dt-1 +... + Dt-n+1) / n, (6-5)
где Dt, Dt-1, и т. д. – фактическое значение прогнозируемого показателя в периоде t, t-1 и т. д.;
Ft+1 – прогнозируемое значение показателя в периоде t+1;
Dt + Dt-1 +... + Dt+1 – суммарное значение показателя за n периодов;
п – число периодов в скользящей средней.
При относительно небольшом числе периодов применение скользящей средней обеспечивает большую чувствительность к изменениям прогнозируемого показателя, однако при этом могут быть неоправданно учтены и его случайные колебания.
Этот метод, так же как и "наивный", прост и быстр в использовании. К его недостаткам можно отнести учет при расчете среднего и более давних, и последних данных с равной степенью значимости.
Метод взвешенной скользящей средней является разновидностью метода скользящих средних и нивелирует вышеуказанный недостаток. В соответствии с этим методом при расчете скользящей средней данным различных периодов присваиваются определенные веса (коэффициенты значимости), отражающие степень их важности для разрабатываемого прогноза, как показано в формуле (6-6). Выбор коэффициента значимости достаточно субъективен, а наиболее адекватное соотношение зачастую приходится выявлять методом проб и ошибок.
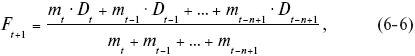
где mt – коэффициент значимости периода t;
mt + mt-1 + ... + mt-n+1 – сумма коэффициентов значимости за n периодов.
Метод экспоненциального сглаживания так же как и предыдущий, является модификацией метода скользящих средних. Согласно ему прогнозное значение показателя определяется с учетом так называемой константы сглаживания а: ее малые значения увеличивают вес данных более ранних периодов, большие значения – более поздних, как показано в формуле (6-7):
Ft+1 = Ft + a • (Dt – Ft), (6-7)
где a – константа сглаживания (0 ? а ? 1);
Ft – прогнозируемое значение показателя в периоде t.
Так же как и в случае взвешенного скользящего среднего, точность прогноза, полученного методом экспоненциального сглаживания, во многом зависит от выбранной величины константы сглаживания – высокие значения этого показателя рекомендуется выбирать при быстром изменении спроса, более низкие – при медленном [Ламбен, 2004]. Наиболее адекватную величину константы сглаживания определяют путем перебора и сравнения полученных результатов прогнозирования с фактическими данными прошлых периодов. Иногда используются и более сложные модификации этого метода с учетом тренда и сезонного регулирования.
Метод экстраполяции временного ряда можно рекомендовать, если для статистических данных за предыдущие периоды характерен определенный тренд – тенденция к росту или уменьшению значений показателя во времени. При этом к имеющимся фактическим данным за предыдущие периоды подбирается определенная линия тренда, выраженная с помощью различных математических уравнений трендов: линейных, степенных, экспоненциальных, логарифмических, полиномиальных и др. Искомый прогноз строится на основании экстраполяции полученной прямой.
Самым простым из уравнений трендов является линейный тренд. Для его определения, так же как и в случае линейной регрессии, может быть использован метод наименьших квадратов (см. формулы (6-1 – 6-3)) с той лишь разницей, что в качестве независимой переменной выступает только фактор времени.
Для некоторых временных рядов характерны определенные сезонные колебания. Под сезонными колебаниями данных временного ряда понимаются "регулярно повторяющиеся восходящие или нисходящие движения в ряду значений, которые можно привязать к периодически повторяющимся событиям" [Стивенсон, 1998, с. 514].
Сезонность во временном ряде выражается в значении, на которое фактическая величина прогнозируемого показателя отклоняется от среднего значения ряда. Сезонные колебания цикличны и повторяются через определенные периоды времени. Так, например, спрос на услуги приморских отелей повышается летом, а спрос на услуги горнолыжных курортов – с декабря по март.
Для определения сезонных колебаний необходима информация о спросе за каждый квартал, месяц, иногда даже за декады. Прогнозирование с учетом сезонных колебаний основывается на предположении, что данные тенденции не изменятся до наступления прогнозируемого периода.
Учет сезонности может быть осуществлен с применением аддитивной или мультипликативной моделей. Аддитивная модель предполагает, что сезонные изменения определяются путем вычитания или добавления соответствующей величины к среднему значению ряда. В мультипликативной модели сезонная компонента (индекс сезонности) умножается на среднее значение ряда.
В табл. 6.1 приведен пример расчета сезонных компонент для прогнозирования спроса.
Таблица 6.1. Пример расчета сезонных компонент для прогнозирования спроса