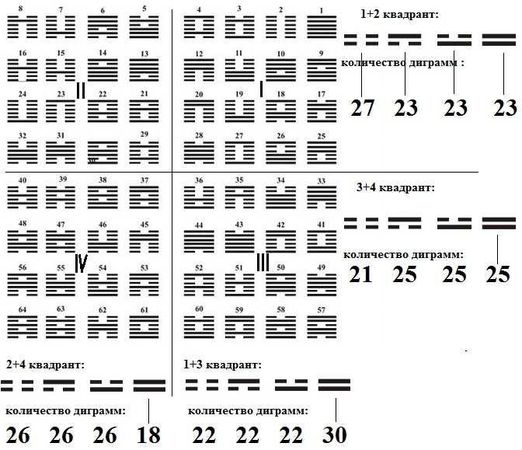
Рис. 18а. Суммы диграмм в двух столбцах и двух строках четырех квадрантов классического квадрата гексаграмм Книги Гуа.
4. Заключение
В данной работе мы увидели:
– закономерности распределения сумм мантических формул "первого слоя" по Ю.К.Щуцкому в классическом квадрате гексаграмм Фу Си; анализ этих закономерностей предполагает оперирование в ранние периоды мантическими формулами, представляющими из себя диграммы, в применении к ряду триграмм по Фу Си; основным базисом этих закономерностей является "распределение Бу ши" сумм формул в строках и столбцах – набор из четырех числовых значений, выстроенный векторно и с выделением, обозначением "внешнего" и "внутреннего" (2453, 6435 и т. д.);
– при построении Книги Гуа Вэнь Вана использовался основной источник – квадрат 64×64, построенный по принципу Фу Си, с применением дихотомий:
1) разбивка множества 4096 додекаграмм на: содержащие зеркальные гексаграммы и инверсные гексаграммы с одной стороны и не содержащие – с другой.
2) множество содержащих додекаграмм из п.1) – 64 штуки – дихотомируем на: относящихся к додекаграммам с Х (32шт.) рисунка 14, 16 б) и – не относящихся (0). Рис. 14 – тоже результат дихотомий: на имеющих признаки "распределения Бу ши" и условия п.3.1.3 – с одной стороны и – не имеющих – с другой (см. Приложение).
3) присутствуют дихотомии, из уже выбранных 32 додекаграм, на принадлежность к областям додекаграмника рис. 13: выше – ниже оси 1\64–64\1, выше – ниже оси 1\1 – 64\64, наружные – внутренние области каждого из шести комплексов рис. 16, шесть комплексов разбиваются на: первые и последние – с одной стороны и внутренние (3-ий и 4-ый) – с другой.
Далее, производится построение типа рис. 6, куда делегируются додекаграммы из областей пункта 3). Это построение также имеет признаки принципа "распределения Бу ши"; присутствует дихотомия на "чет" – "нечет" нового построения из додекаграмм от областей додекаграмника: выше оси 1\64–64\1 – ниже оси 1\64–64\1, первые десять – вторые десять – из множества наружных в шести комплексах также выше-ниже оси 1\1-64\64), дихотомия на минимальные и максимальные: числа корреспонденций по инверсности додекаграмм между четырьмя "двумя строками" Книги Гуа, промежутков (рис. 18), в виде количеств разделяющих додекаграмм, при размещении в Книге Гуа, между инверсными додекаграммами каждого из шести комплексов;
– мантические формулы в Книге Гуа, имеющие набор из всех четырех терминов корреспондированы (вместе со своими додекаграммами, естественно) в первый квадрант; все остальные формулы разделены поровну между первой и второй половиной по принципу равенства количеств терминов – по восемь формул с одним термином, по три формулы с двумя терминами, по две формулы с тремя терминами – все как в классическом квадрате гексаграмм Фу Си.
– последовательность построения Книги Гуа, вероятно не единожды корректирующаяся, разбита на этапы, зоны применения вышеуказанных характеристик:
а) построение "первых двух строк" – по принципу последовательного перемещения по наружным элементам комплексов рис. 16, соблюдения зон "чета" – "нечета" и принципу минимизации корреспонденций по инверсности додекаграмм в другие "две строки". б) первый квадрант – по принципу размещения в нем всех формул с четырьмя терминами, симметрии осевых додекаграмм и "счета до десяти" в) окончательная достройка первой половины – принципы равенства количеств формул с одинаковым счетом терминов в нижней и верхней половине Книги Гуа и "счета до двадцати", не забываем, также, про "чет – нечет" г) нижние две строки – по принципу минимизации корреспонденций по инверсности додекаграмм, и главное – размещение 8 формул в виде "фирменной картинки".
д) построение "третьих двух строк" – по принципам последовательного уменьшения "промежутков" между минимальными в комплексах инверсных додекаграмм и соблюдения "правила вектора" рис. 18.
Первая додекаграмма "Посещение" из первого комплекса поменялась местами с додекаграммой "Начальная трудность" из того же комплекса, да и сам первый комплекс, состоящий ранее (в выбранном прототипе из Приложения ) из инверсных пар с неизменяющейся векторностью стал смешанным (рис. 14, 16б). Последняя пара додекаграмм нашего построения "Выступление" и "Воссоединение" также поменялись местами, но – изменив свою четность – это вторая смена четности, первая смена, как мы помним, произошла для установления комбинации мантических формул нижних "двух строк". Воистину: исключения из правил, подтверждающие правила!
Конечно остались вопросы:
– был ли искусственным перенос формул "свершение" в трех гексаграммах рис. 8?
– или этот экстремум в двух центральных столбцах был изначально предустановлен? Я склоняюсь к тому, что перенос был, но проследить пошаговую логику переноса с гармонизацией построения формул в "четвертых двух строках" несколько затруднительно. Здесь любопытно следующее: в рис. 17 (в нем последовательность номеров Фу Си в каждом комплексе – "распределение Бу ши") присутствует удивительная симметрия расположения додекаграмм, где эти переносы состоялись– из 21 додекаграммы 4-го комплекса в 20 додекаграмму 3-го комплекса; из 15 додекаграммы 5-го комплекса в 28 додекаграмму второго комплекса; из 37 додекаграммы 2-го комплекса в 50 додекаграмму 5-го комплекса. И приходится признать, что выбор в построении "четвертых двух строк" додекаграмм с минимальным числом корреспонденций по инверсности (додекаграммы "Начальная трудность" – "Смена"), является более приоритетным, чем сохранность трех формул.
– насколько глубоко мы можем восстановить, для изучения, параметры применения и формирования четырех множеств скорреспондированных в "распределение Бу ши"? Есть ли еще аналоги их применения в других артефактах?
– какой смысл несет в себе дихотомия на "минимальное" и "максимальное"? В "распределении Бу ши" результатов манипуляций на тысячелистнике, "минимальная" вероятность выпадения 6 и 9 рассматривается, как активно изменяющаяся (сама) "старая" часть, "максимальное" – это то "молодое", что изменяется, растет под действием "минимального". Результатом же этой установки является увеличение числа черт сяо "инь" и уменьшение числа вероятности получения черт сяо "ян", которая, вследствии своей минимальности, приобретает способность к более "активному" собственному изменению. Удастся ли воспроизвести при этом сопровождающее суждение в адекватном варианте – большой вопрос. Но существует множество построений, где данная дихотомия присутствует вне векторного содержания.
Хотелось бы добавить, что ход описанных здесь рассуждений, показывает лишь логичный и пошаговый способ построения, вытекающий из обнаруженных фактов (отображенных в рис. 1, рис. 8, рис. 14, Приложении ), и не претендует на точность воспроизведения последовательности рассуждений, происшедших в 1121 году до нашей эры.
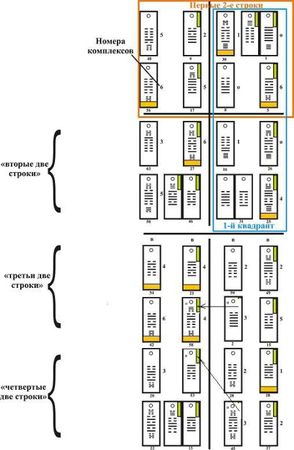
Рис. 19 На этом рисунке изображены бамбуковые дощечки весьма условно, в попытке показать возможность отображения: свойства нечетности додекаграмм (в Книге гуа) в додекаграмнике рис. 1б) (метка справа вверху), векторность додекаграмм (рис. 14) или, что то же самое – четность гексаграмм – отверстие вверху, изменение векторности в паре инверсных додекаграмм (метка внизу). Фактически, как можем понять, метки на планках м.б. какими угодно.
Приложение
Здесь мы рассматриваем варианты выбора (приоритет рис. 14) между различными комбинациями расположения одной из двух (помечено – Х) зеркальных (для номеров гексаграмм) додекаграмм – находящихся симметрично оси 1\1 – 64\64 (например, выбор между додекаграммами 32 и 63 рис. 16а). Рассмотрим варианты комбинаций для сумм додекаграмм, имеющих такие же числовые значения векторов (2453 и 5346), как и суммы мантических формул в квадрате гексаграмм Фу Си (рис. 8). Отсюда, кстати, следует вторичность применения данного "распределения Бу ши" в квадрате додекаграмника Фу Си после "первичности" его применения в квадрате гексаграмм Фу Си (а еще раньше – в мантических формулах в рядах триграмм). Хотя… окончательно, со 100 % уверенностью, вопрос "первичности" не м.б. утверждаем. Всегда есть вероятность того, что источником данных, 2 4 5 3 и 5 3 4 6, числовых распределений являются другие, неведомые нам материалы. Будем рассматривать с ограничениями: наличием осевого содержания рис. 13 б) и нижней строки рис. 15. Таких вариантов – несколько тысяч. Но мы введем еще ограничения: во втором и третьем квадранте расположение пар инверсных додекаграмм симметрично относительно центра додекаграмника 0 (пары инверсных додекаграмм с неизмененной векторностью, углы каждого комплекса (по рис. 16 а) данных квадрантов помечены буквой б) . Это ограничение дает нам четырнадцать комбинаций (представленных ниже), из которых только три (последние) имеют два комплекса – четвертый и шестой – с полностью изменяющимися векторами в инверсных парах додекаграмм (помечены буквой ж ). Комбинаций со всеми тремя комплексами -4, 5, 6– (из рис. 16 а) в первом и четвертом квадранте, которые бы были с полностью изменившимися векторами в инверсных парах додекаграмм (ж) (на рис. 6 -это пары темного цвета, за исключением второй и двадцать пятой додекаграммы, помеченных римскими цифрами) и сохраняли бы данные "распределения Бу ши" – нет.

В этих шести додекаграммниках, только у четырех есть (и всего один) комплекс (шестой), в котором все инверсные пары имеют измененную векторность в додекаграммах (они симметричны оси 1\64–64\1). Вероятно, этот факт не очень устраивал Вэнь Вана, и он попробовал изменить векторность "распределения Бу ши" сумм додекаграмм в верхней половине додекаграммника.

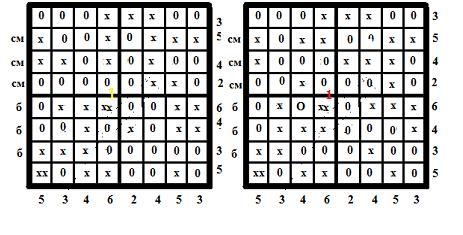
Всего здесь присутствует восемь додекаграммников и среди них найдено только три варианта с более ярко выраженной (аж два комплекса: 4 и 6) измененной векторностью в инверсных парах, и один из трех (первый) имеет относительную оси 1\64–64\1 симметрию сумм в квадратиках более крупного плана. Он и был выбран, как прототип известного нам расположения на рис. 14.

В общем-то, в этом Приложении использовался элементарный (и не компьютерный) перебор, структурированных, по известным признакам, расположений, имеющих конечное и не очень большое количество вариантов; уж во всяком случае, не несколько тысяч (и уж точно, не два в тридцать второй степени 232) вариантов других просчетов.
Конец © Подоплелов С.И., 2012