3. Налог на прибыль
Прибыль = 75 (доходы без НДС) – 25 (стоимость материалов без НДС) – 28 (фонд оплаты труда со всеми налогами) – 5 (транспортировка) – 2 (амортизация) – 8 (другие затраты) = 7 тысяч гривен.
Налог на прибыль = 7 × 18 % = 1,26 тысяч.
Чистая прибыль = 7–1,26 = 5,74 тысяч гривен.
По основным налогам уплачено 10 + 10,832 + 1,26 = 22,1 тысячи гривен.
Взгляните на это соотношение чистой прибыли и уплаченных налогов. Если вам показалось, что налоги чересчур высоки и справедливей было бы недоплатить их и получить немного больше прибыли, то вы сделали первый шаг на пути к налоговой оптимизации. Остановились бы вы на законных методах оптимизации налогообложения (например, предложили бы сотрудникам стать частными предпринимателями с упрощённой системой налогообложения и оплачивали бы их услуги) или пошли бы дальше, кто знает, не так ли?
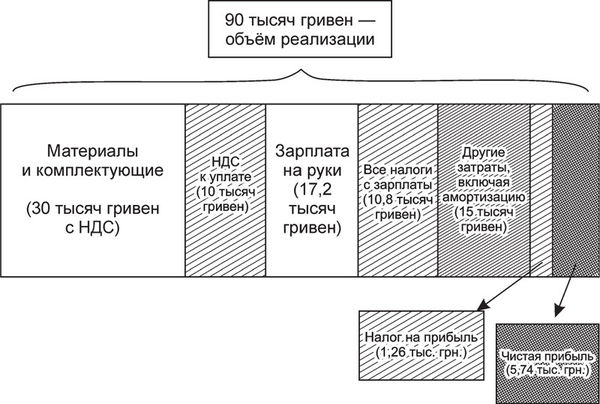
Налоги в структуре финансовых показателей деятельности предприятия
Стоимость денег во времени
Концепция стоимости денег во времени пронизывает понимание множества экономических процессов. Движение капиталов в мире и внутри страны, решение об инвестициях, приоритет краткосрочным или длительным проектам, оценка стоимости бизнеса и многое другое.
Эволюция человеческого мозга длится уже миллионы лет, а экономическими расчётами человек занялся сравнительно недавно. Поэтому некоторые функции и оценки мы производим практически автоматически, сами не понимаем, как это происходит. А другие, среди которых и финансовые расчёты, для множества людей представляют реальную проблему.
Концепция стоимости денег во времени не является интуитивно понятной. Потребуются определённые усилия, чтобы принять её логику. Тем не менее, она весьма важна, а её методы и механизмы являются своего рода стандартом коммуникации в современной экономике.
Финансы – это своего рода язык, благодаря которому люди в разных уголках земного шара могут понять друг друга. В современном мире, когда экономика стирает границы отношений, это крайне важно.
Финансовая математика. Сложный процент
Представьте себе, что положили в банк 1000 гривен под 20 % годовых на 1 год. Через год вы будете обладать суммой 1200 гривен. А что, если вы оставите эту сумму ещё на год? Тогда проценты будут начисляться на общую сумму 1200 и составят 1200 × 20 % = 240 гривен. А общая сумма вклада будет 1200 + 240 = 1440 гривен.
Если проследить, что будет происходить с суммой вклада и процентами, то получим такую последовательность относительно общей суммы, которой мы владеем:
Рост суммы вклада при реинвестировании процентов (ставка = 20 % годовых):
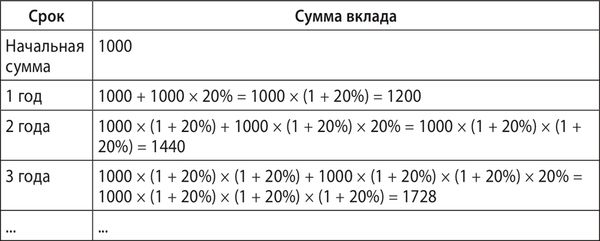
Наблюдая за ростом суммы на вкладе, можно прийти к такой закономерности: при реинвестировании процентов по вкладу сумма на конец периода будет составлять
S = S0 × (1 + w),
где S – сумма вклада на конец периода;
S0 – начальная сумма вклада;
w – ставка процента, под которую инвестирована сумма S0;
t – период времени (срок) вклада.
Это так называемая формула сложных процентов. Чтобы посчитать, какой суммой мы будем обладать через 5 лет, подставляем значения в формулу:
S = 1000 × (1 + 20 %) = 2488,32 гривен.
А через 100 лет?
S = 1000 × (1 + 20 %) = 82817974522 гривен (более 82 миллиардов гривен).
Впечатляет, не так ли? Сложные проценты на длительных временных отрезках выдают настолько впечатляющие цифры, что люди порой отказываются им верить. Например, если бы в момент рождения Иисуса Христа мы положили бы 1 цент под 5 % годовых, то через 2015 лет имели бы цифру с сорока нулями после запятой. Здесь своего рода проблема нашего мышления и восприятия. Мы мыслим сегодняшними деньгами и изначально невыполнимую установку об одном центе воспринимаем как данность.
Из категории сложных процентов возникают другие экономические последствия, а именно:
1. Деньги под матрасом или в тумбочке теряют свою стоимость. Когда деньги не попадают в экономику, вы утрачиваете альтернативную доходность.
2. Процентные ставки, как мы помним, зависят от уровня риска. Поэтому в рискованной ситуации, на рисковой территории вы должны предложить потенциальному инвестору действительно высокую отдачу на инвестиции в будущем, ведь иначе он предпочтёт другие альтернативы.
3. Небольшие преимущества преумножаются и дают весомый эффект благодаря мультипликативному эффекту сложного процента.
4. Чрезмерно высокие ставки существенно ограничивают число проектов, претендующих на финансирование в силу того, что не способны дать высокий ожидаемый эффект.
Также приведём пример того, как банки могут использовать недостаточное знание людей о работе сложного процента. Например, банк предлагает альтернативу – положить деньги на вклад под 25 % годовых с начислением процентов в конце срока или сделать вклад с ежемесячным начислением процентов по 24 % годовых. Зная, что проценты мы можем реинвестировать, мы можем посчитать, сколько же мы получим по второму вкладу через год, добавляя каждый месяц проценты к вкладу.
Итак, S = S0 × (1 + 24 % / 12) = 1,268 × S0.
Мы видим, что несмотря на кажущуюся более низкую процентную ставку, наш вклад растёт на 26,8 %, что больше первого предложения 25 % годовых.
Поэтому понимание механизма сложных процентов важно и при обычных бытовых финансовых вопросах.
Чистая теперешняя стоимость, или Когда два плюс два не равно четыре
Мы разобрались, как преумножаются деньги, вложенные под процент, и как сравнить два вклада с идентичными сроками действия. Но жизнь, естественно, менее линейна, гораздо чаще в ней встречаются более сложные для сравнения условия.
Так, типичный инвестиционный проект (покупка оборудования, строительство здания, расширение деятельности, другое) выглядит, как правило, так: сегодня инвестируешь в предполагаемые будущие преимущества, в будущем пользуешься ими.
Начнём с простого примера. Вам предлагают отдать кому-то миллион, а получить взамен 700 тысяч через год и ещё 700 тысяч через два года с момента инвестиции. Как нам подойти к оценке этой сделки, если альтернативой является положить деньги под 20 % годовых на депозит?
Вернёмся к нашей формуле S = S0 × (1 + w).
Из этой формулы S0 = S / (1 + w).
Задумаемся над экономическим смыслом этой формулы. Она означает, что будущая сумма в размере S равна по ценности сегодняшней сумме в размере S0. 120 тысяч через год равны 100 тысячам сегодня.
Исходя из этой предпосылки, мы, например, не можем сложить 700 тысяч через год и 700 тысяч через два года, так как ценность их не одинакова.
В финансах нашли решение этой проблемы, и выглядит оно так. Все будущие денежные потоки должны быть приведены к сегодняшней стоимости. Только после этого с ними можно производить математические действия.
Исходя из альтернативы в виде ставки в 20 % стоимость 700 тысяч через год будет соответствовать 700 / 1,2 = 583,3 тыс. гривен сегодня, а стоимость 700 тысяч через два года 700 / 1,2 = 486,1 тыс.
700 + 700 превратились в 583,3 + 486,1 = 1069,4.
То есть нам предлагают дать сегодня миллион, чтобы получить в сегодняшних деньгах 1069,4 тыс. гривен, что больше миллиона. Сделка выглядит интересной, ведь получаем больше, чем даём.
Стоимость денег во времени и теперешняя стоимость могут вгонять сознание в своего рода "ступор", ведь согласно им мы не имеем права складывать денежные потоки, которые находятся в разных временных отрезках.
Мы должны привести их к сегодняшней стоимости и лишь затем производить с ними математические действия.
Деньги завтра всегда менее ценны, чем деньги сегодня. Чем выше риски, тем выше требуемая ставка доходности. Чем выше ставка доходности, тем ниже стоимость будущих ожиданий.
Практика показывает, что приведение будущих ожиданий к сегодняшней стоимости весьма непросто даётся нашему мозгу. Как 700 + 700 могут стать 1069,4, с одной стороны, кажется логически понятным, с другой стороны, вызывает недоверие. И всё же отнесём этот факт сложности восприятия к нетипичной для нашего мозга операции.
Показатели инвестиционной привлекательности проекта
Приведение будущих ожиданий к их сегодняшней стоимости называется дисконтированием. Для оценки будущих выгод в сегодняшней стоимости используется дисконт (скидка), что мы увидели в примере выше.
Для оценки инвестиционной привлекательности проекта, будь то новое предприятие или проект в рамках существующего предприятия, используются такие основные показатели оценки:
1. NPV (Чистая теперешняя стоимость).
2. IRR (Внутренняя ставка доходности).
3. DPB (Дисконтируемый период окупаемости).
Рассмотрим такой проект.
Предприятие может модернизировать своё оборудование, вложив для этого 6 миллионов гривен. Эффект от модернизации будет наблюдаться в течение 6 лет, позволяя экономить ежегодно 2 миллиона гривен. Необходимо оценить инвестиционную привлекательность проекта, если предприятие выставляет требование к возврату на инвестиции для проектов с таким уровнем риска как 20 % годовых.
1. Чистая теперешняя стоимость (NPV).