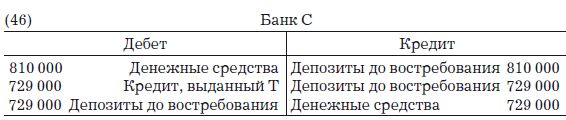
А баланс банка С приобретет следующий вид:
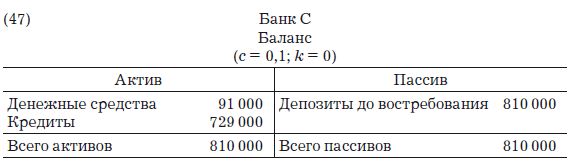
Когда Т заплатит своему кредитору S, при том что S хранит свои деньги в мелком банке D (у которого точно так же c = 0,1, а k = 0), будут сделаны бухгалтерские записи:
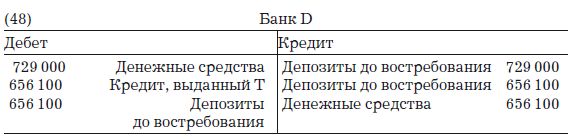
А баланс банка D станет выглядеть следующим образом:
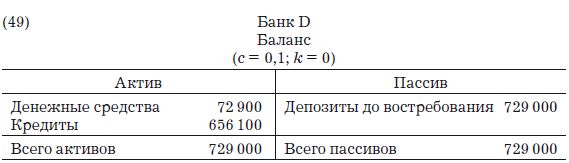
Общая сумма депозитов в системе очень малых банков равна сумме последовательности, отраженной в формуле [8], которая относится к банку-монополисту:
[26] 1 000 000 + 1 000 000 · 0,9 + 1 000 000 · 0,9 +1 000 000 · 0,9 + … = 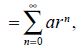
где: a = 1 000 000;
r = 0,9.
Как показано в прим. 27, эта сумма, в свою очередь, равна:
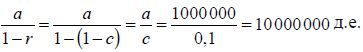
А поскольку a = d = 1 000 000 д.е., вложенных первоначально, то общую сумму депозитов можно рассчитать по формуле
[27] 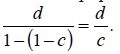
Эта формула идентична мультипликатору депозитов для случая банковской системы, состоящей из единственного банка-монополиста [14].
Теперь вспомним, что
[28] 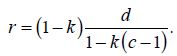
Так как банковская система в этом случае состоит из мелких банков и k = 0, то, подставив значение k в формулу [28], получим, что r = 1 – c = = 0,9, что нам уже известно. Поэтому банковская система, составленная из малых банков, порождает в общей сложности объем депозитов в размере 10 000 000 д.е. и чистую кредитную экспансию в размере 9 000 000 д.е., идентичные тем, что порождает монополистический банк с k = 1. Полученные результаты сведены в табл. 4–2.
Система мелких банков (где k = 0), конечно же, является исключением в рамках банковской системы вообще, где 0 < k < 1. Однако этот пример прост для понимания и поэтому обычно используется в учебниках для объяснения создания кредитных денег финансовой системой.
Таблица 4-2
Система мелких банков
(k = 0,2; c= 0,1)
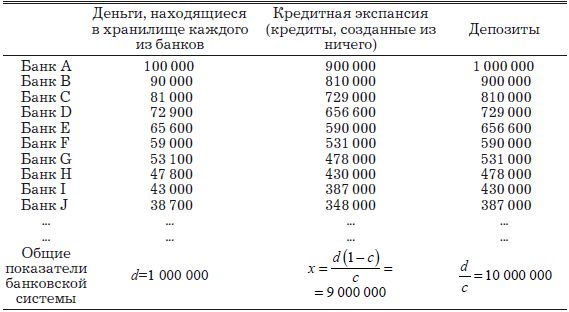
Примечание: Последние три цифры округлены.
Верно также и то, что банковская система, состоящая из банка-монополиста (когда k = 1), – уникальный случай в рамках более широкой категории изолированных банков, расширяющих депозиты и кредиты.
В заключение отметим, что два частных случая ведут к идентичным результатам в том, что касается создания новых кредитов (9 000 000 д.е.) и общего объема депозитов (10 000 000 д.е.). В первом случае была рассмотрена система мелких банков с k = 0. Второй случай – изолированный банк с k = 1. С учетом того, что эти примеры просты для понимания, они обычно используются в учебниках для объяснения создания кредитов и объема депозитов, генерируемых банковской системой. Разные авторы ссылаются либо на систему крохотных банков, либо на единственный банк-монополист (или на банк, чьими клиентами являются конечные получатели кредитов).
6 Некоторые дополнительные сложные случаи
Когда экспансию начинают все банки одновременно
В свете того факта, что в данном контексте мы вынуждены предложить упрощенный взгляд на процесс кредитной экспансии, необходимо отметить несколько дополнительных моментов, а также сделать некоторые пояснения. Начнем с того, что описанные нами процессы экспансии целиком и полностью возникают исключительно в результате увеличения количества денег, внесенных на вклад в начальном банке (в нашем примере d представляет 1 000 000 д.е., депонированных в банке А). Однако и исторически, по мере развития банков, и в настоящее время все процессы кредитной экспансии характеризуются тем, что новые деньги вливаются в банковскую систему не через один-единственный банк, а через множество банков (а то и в той или иной степени через все банки системы). Как показывает Ричард Липси, кредитная экспансия, подобная описанной нами – происходящая ex nihilo и поддерживаемая созданием необходимых банковских депозитов, – будет повторяться всякий раз, когда в любом из банков будет делаться вклад в размере 1 000 000 д.е. Поэтому общий процесс экспансии на деле является более существенным по масштабам и качественно более сложным, так как он происходит одновременно во многих банках и от множества депозитов. В нашем единственном примере с коэффициентом резервирования 10 % в итоге были созданы кредиты на сумму 9 000 000 д.е., что в девять раз превышает начальный депозит, и в результате денежное предложение увеличивается в 10 раз. Главный вывод, который отсюда следует, состоит в том, что если все банки одновременно получат новые денежные депозиты, они смогут расширить кредит без уменьшения своих денежных резервов, потому что, предоставляя кредиты, ведущие к изъятию денег (как мы до сих пор предполагали в наших бухгалтерских записях), они одновременно получают депозит в виде части денег, предоставленных в виде кредитов другими банками. Следовательно, на деле вовсе не обязательно происходит значительное сокращение резервов каждого из банков, и каждый банк, поддерживая свои резервы практически в неприкосновенности, будет способен выдавать кредиты и соответственно создавать депозиты, без особого риска.
Этот теоретический аргумент побудил многих авторов, и в том числе Мюррея Ротбарда, при рассмотрении процесса кредитной экспансии в банковской системе исходить из того, что изолированный банк не теряет резервов при предоставлении все новых кредитов. Напротив, сохраняя резервы в неприкосновенности, изолированный банк изо всех сил пытается выдать новые кредиты на сумму, кратность которой по отношению к резервам обратно пропорциональна коэффициенту резервирования. Аргумент, объясняющий такой вид банковского мультипликатора, даже для случая изолированного банка, состоит в том, что банк будет пытаться избежать сокращения своих резервов в процессе предоставления кредитов (т. е. банкир не захочет оставить 100 000 д.е., а 900 000 д.е. ссудить). Напротив, для банка куда выгодней поддержание своего коэффициента резервирования путем предоставления кредитов на как можно более крупную сумму и сохранение начального резерва наличности в неприкосновенности (т. е. храня 1 000 000 д.е. наличными и создав из ничего новые кредиты на 9 000 000 д.е.). На практике уровень резервов наличности может быть обеспечен, если процесс кредитной экспансии протекает одновременно во всех банках. Это происходит оттого, что уменьшение наличности, которое банк испытывает после предоставления кредитов, компенсируется приемом новых депозитов, берущих начало из кредитов, взятых в других банках.