Рис. 3.19.Параллельное соединение двух катушек индуктивности
![]()
Рис. 3.20.Последовательное соединение трёх катушек индуктивности
Рис. 3.21.Параллельное соединение трех катушек индуктивности
Формулы для вычисления общей индуктивности при последовательном и параллельном включении похожи на аналогичные формулы для вычисления общего сопротивления резисторов.
Если при изготовлении какого-либо прибора у вас не оказалось нужной индуктивности, но имеется большое количество катушек индуктивности других номиналов, их можно соединить последовательно или параллельно для получения нужного номинала. При последовательном соединении вычисления довольно простые, а вот при параллельном соединении необходимо затратить время на вычисления. Тоже самое приходится делать при последовательном соединении конденсаторов и при параллельном соединении резисторов. Для облегчения подбора второго элемента на рис. 2.22 (глава 2) приведена номограмма.
3.2.7. Катушка индуктивности как накопитель магнитной энергии
В этом эксперименте в качестве катушки индуктивности можно использовать первичную обмотку сетевого трансформатора. При замыкании выключателя SA лампочка еле светится, а при размыкании выключателя SA она ярко вспыхивает. Это объясняется тем, что в момент включения элемента G часть энергии источника тратилась на создание магнитного толя катушки индуктивности, а при размыкании выключателя магнитное поле катушки индуктивности исчезает и запасенная в ней энергия отдается лампочке. Это явление называется самоиндукцией. Э.д. с самоиндукции препятствует увеличению тока при подключении источника питания к катушке индуктивности, а при отключении источника питания э.д.с. самоиндукции препятствует уменьшению тока в катушке. Здесь имеется ввиду, что все элементы включены последовательно.
3.2.8. Сила тока отстает от напряжения на катушке индуктивности на угол π/2
Так как i = ImSinωt, a u = UmSin (ωt - π/2), то, следовательно, напряжение на катушке индуктивности опережает силу тока по фазе на угол π/2. Это видно также на векторный (рис. 3.22, а) и на временной (рис. 3.22, б) диаграммах.
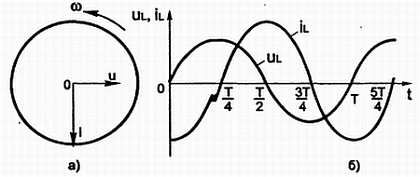
Рис. 3.22.Напряжение на катушке индуктивности опережает силу тока по фазе на угол 90°.
3.2.9. На активном сопротивлении (на резисторе) сила тока и напряжение совпадают по фазе
Так как i = ImSinωt, и u = UmSinωt, то, следовательно, напряжение на резисторе совпадает по фазе с силой тока. Это видно также на векторной (рис. 3.23, а) и на временной (рис. 3.23, б) диаграммах.
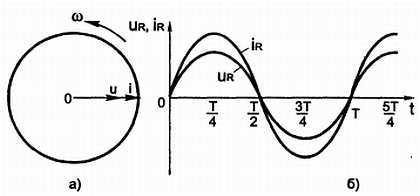
Рис. 3.23. Напряжение на резисторе совпадает по фазе с силой тока
3.3. ИНТЕГРИРУЮЩИЕ И ДИФФЕРЕНЦИРУЮЩИЕ ЦЕПИ
В электронных устройствах часто бывает необходимо изменить прямоугольные импульсы или сигналы другой формы таким образом, чтобы получить сигнал требуемой формы. Указанное изменение может заключаться в сохранении высокочастотных составляющих сигнала и ослаблении низкочастотных составляющих, в ослаблении только высокочастотных составляющих, в изменении амплитуды и формы сигнала путем ограничения и т. д.
К таким устройствам можно отнести интегрирующую и дифференцирующую цепи, которые находят широкое применение в вычислительной технике, в системах развертки телевизионных приемников и в других случаях, когда необходимо ослабить высокочастотных составляющие импульсов.
Практически интегрирующую цепь (рис. 3.24, а.) можно рассматривать как фильтр нижних частот. При воздействии синусоидальных сигналов интегрирующая цепь сильнее ослабляет сигналы более высоких частот (и вносит некоторый фазовый сдвиг). В случае импульсных или прямоугольных сигналов их форма изменяется благодаря фильтрации высокочастотных сигналов.
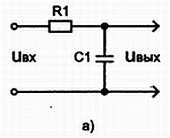
Рис. 3.24, а) Cxeма интегрирующей цепи
В практических схемах интегрирующих цепей постоянная времени t = RC велика по сравнению с длительностью воздействующего импульса. В этом случае при ращение напряжения ес на конденсаторе мало по сравнению с напряжением е, приложенным к интегрирующей цепи. Тогда можно записать приближенное равенство:
![]()
Таким образом, выходное напряжение интегрирующей цепи пропорционально интегралу входного тока e/R. Это можно объяснить, если обратиться к рис. 3.24, б и в.
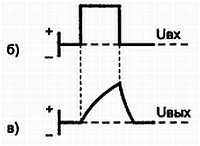
Рис. 3.24, б) форма входного импульса интегрирующей цепи, в) выходного импульса интегрирующей цепи
При подаче на вход схемы положительного импульса крутой фронт импульса действует на интегратор в течение очень короткого промежутка времени. Затем в течение времени, равного длительности импульса, действует напряжение, соответствующее плоской вершине импульса. Напряжение на конденсаторе нарастает по экспоненциальному закону. За время, равное постоянной времени цепи τ, напряжение на конденсаторе достигнет примерно 65 % максимального значения, а полностью конденсатор зарядится примерно в течение пяти постоянных времени (5τ). Так как постоянная времени интегрирующей цепи велика по сравнению с длительностью импульса, напряжение на конденсаторе не достигает максимального значения, а постепенно нарастает до некоторой величины (рис. 3.24, в).
По окончании действия входного импульса конденсатор начнет разряжаться через резистор R1 и входную цепь. Разряд протекает медленно по сравнению со спадом входного импульса, и в результате на выходе формируется импульс, форма которого показана на рис. 3.24, в.
Если импульсы на входе интегратора имеют длительность, превышающую интервалы между ними (рис. 3.24, г), то напряжение на конденсаторе будет постепенно нарастать.
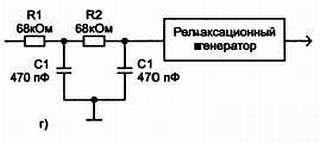
Рис. 3.24, г) длительность входных импульсов превышает интервал между ними

Такую схему можно использовать в качестве делителя частоты, так как уровень запуска релаксационного генератора будет достигаться только после определенного числа импульсов, поданных на вход. Постоянная времени этой цепи равна:
τ ~= R1(C1 + С2) + R2C2.
Интегрирующую цепь можно также построить, располагая катушкой индуктивности и резистором. Для этого в схеме на рис. 3.24, а резистор R1 следует заменить катушкой индуктивности, а конденсатор С1 - резистором. Однако, поскольку катушка индуктивности имеет еще и активное сопротивление, схема с резистором и конденсатором более широко применяется на практике.
В дифференцирующей цепи (рис. 3.25, а) постоянная времени должна быть малой по сравнению с длительностью импульсов.
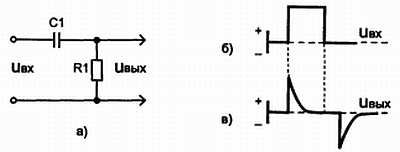
Рис. 3.25. а) Схема дифференцирующей цепи б) форма импульса на входе дифференцирующей цепи в) выходе дифференцирующей цепи
Эту цепь применяют в тех случаях, когда импульсы сравнительно большой длительности необходимо преобразовать в короткие импульсы с крутым фронтом. Цепь сохраняет крутой фронт импульса в той же полярности и по существу ведет себя как фильтр верхних частот, ослабляющий низкочастотные и пропускающий высокочастотные составляющие импульса.
При малой постоянной времени сопротивление резистора оказывается значительно больше реактивного сопротивления конденсатора. Поэтому выходное напряжение, равное падению напряжения на резисторе, приближенно выражается формулой: