Речь идет о квантовой суперпозиции (когерентной суперпозиции), то есть о суперпозиции состояний, которые не могут быть реализованы одновременно с классической точки зрения. Суперпозиционные состояния могут существовать лишь при отсутствии взаимодействия рассматриваемой системы с окружением. Они описываются посредством так называемой волновой функции, которую также называют вектором состояния. Это описание формализуется заданием вектора в гильбертовом пространстве , определяющим полный набор состояний, в которых может находиться замкнутая система.
Волновая функция - это частный случай, одна из возможных форм представления вектора состояния как функции координат и времени. Это представление системы, максимально приближенное к привычному классическому описанию, предполагающему наличие общего и независимого ни от чего пространства - времени.
Наличие этих двух типов состояний - смеси и суперпозиции - является основой для понимания квантовой картины мира и ее связи с мистической. Другой важной для нас темой будут условия перехода суперпозиции состояний в смесь и наоборот. Эти и другие вопросы мы разберем на примере знаменитого двухщелевого эксперимента .
Для начала возьмем пулемет и мысленно проведем эксперимент, показанный на рис. 1.
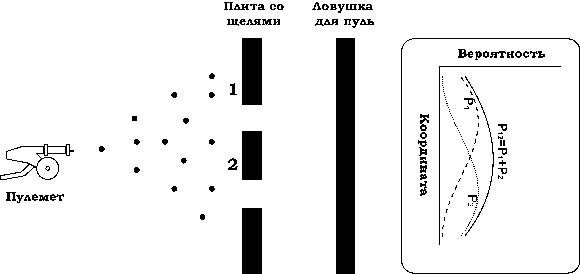
Рис. 1
Он не очень хорош, наш пулемет. Он выпускает пули, направление полета которых заранее неизвестно. То ли направо они полетят, то ли налево…. Перед пулеметом стоит броневая плита, а в ней проделаны две щели, через которые пули свободно проходят. Далее стоит "детектор" - любая ловушка, в которой застревают все попавшие в нее пули. По окончании эксперимента можно пересчитать число пуль, застрявших в ловушке, на единицу ее длины и разделить это число на общее количество выпущенных пуль. Или на время стрельбы, если скорость стрельбы считать постоянной. Эту величину - число застрявших пуль на единицу длины ловушки в окрестности некоторой точки Х , отнесенное к полному числу пуль, мы будем называть вероятностью попадания пули в точку Х . Заметим, что мы можем говорить только о вероятности - нельзя сказать определенно, куда попадет очередная пуля. И даже попав в дыру, она может срикошетить от ее края и уйти вообще неизвестно куда.
Мысленно проведем три опыта: первый - когда открыта первая щель, а вторая закрыта; второй - когда открыта вторая щель, а первая закрыта. И, наконец, третий опыт - когда обе щели открыты.
Результат нашего первого "эксперимента" показан на том же рисунке, на графике. Ось вероятности в нём отложена вправо, а координата - это и есть положение точки X . Пунктирная линия показывает распределение вероятности P 1 попавших в детектор пуль при открытой первой щели, кривая из точек - вероятность попадания в детектор пуль при открытой второй щели и сплошная линия - вероятность попадания в детектор пуль при обеих открытых щелях, которую мы обозначили как P 12 . Сравнив величины P 1 , P 2 и P 12 , мы можем сделать вывод, что вероятности просто складываются,
P 1 + P 2 = P 12 .
Итак, для пуль воздействие двух одновременно открытых щелей складывается из воздействия каждой щели в отдельности.
Представим себе такой же опыт с электронами, схема которого показана на рис. 2.
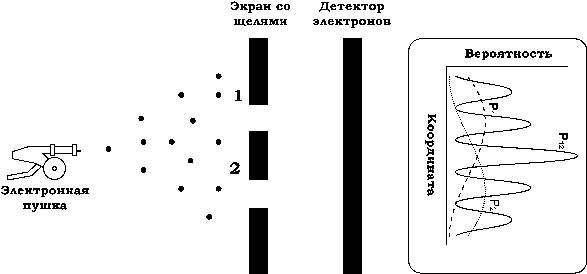
Рис. 2
Возьмём электронную пушку, наподобие тех, что когда-то стояли в каждом телевизоре, и поместим перед нею непрозрачный для электронов экран с двумя щелями. Прошедшие через щели электроны можно регистрировать различными методами: с помощью сцинтиллирующего экрана, попадание электрона на который вызывает вспышку света, фотопленки или с помощью счетчиков различных типов, например, счетчика Гейгера.
Результаты подсчетов в случае, когда одна из щелей закрыта, вполне предсказуемы и очень похожи на итоги пулеметной стрельбы (линии из точек и штрихов на рисунке). А вот в случае, когда обе щели открыты, мы получаем совершенно неожиданную кривую P 12 , показанную сплошной линией. Она явно не совпадает с суммой P 1 и P 2 ! Получившуюся кривую называют интерференционной картиной от двух щелей.
Давайте попробуем разобраться, в чём тут дело. Если мы исходим из гипотезы, что электрон проходит либо через щель 1, либо через щель 2, то в случае двух открытых щелей мы должны получить сумму вкладов от одной и другой щели, как это имело место в опыте с пулеметной стрельбой. Вероятности независимых событий складываются, и в этом случае мы бы получили P 1 + P 2 = P 12 . Во избежание недоразумений отметим, что графики отражают вероятность попадания электрона в определенную точку детектора. Если пренебречь статистическими ошибками, эти графики не зависят от полного числа зарегистрированных частиц.
Может, мы не учли какой-нибудь существенный эффект, и суперпозиция состояний (то есть одновременное прохождение электрона через две щели) здесь совсем не при чём? Может быть, у нас очень мощный поток электронов, и разные электроны, проходя через разные щели, как-то искажают движение друг друга? Для проверки этой гипотезы надо модернизировать электронную пушку так, чтобы электроны вылетали из нее достаточно редко. Скажем, не чаще, чем раз в полчаса. За это время каждый электрон уж точно пролетит всё расстояние от пушки до детектора и будет зарегистрирован. Так что никакого взаимного влияния летящих электронов друг на друга не будет!
Сказано - сделано. Мы модернизировали электронную пушку и полгода провели возле установки, проводя эксперимент и набирая необходимую статистику. Каков же результат? Он ничуть не изменился.
Но, может быть, электроны каким-то образом блуждают от отверстия к отверстию и только потом достигают детектора? Это объяснение также не подходит: на кривой P 12 при двух открытых щелях есть точки, в которые попадает значительно меньше электронов, чем при любой из открытых щелей. И наоборот, есть точки, вероятность попадания электронов в которые более чем вдвое превышает вероятность попадания электронов, прошедших через каждую щель по отдельности.
Стало быть, утверждение о том, что электроны проходят либо сквозь щель 1, либо сквозь щель 2, неверно. Они проходят через обе щели одновременно. И очень простой математический аппарат, описывающий такой процесс, дает абсолютно точное согласие с экспериментом, показанным сплошной линией на графике.
Если подойти к вопросу более строго, то утверждение, что электрон проходит одновременно через две щели, неверно. Понятие "электрон" можно соотнести только с локальным объектом (смешанным, "проявленным" состоянием), здесь же мы имеем дело с квантовой суперпозицией различных компонент волновой функции.
Чем же отличаются пули от электронов? С точки зрения квантовой механики - ничем. Только, как показывают расчеты, интерференционная картина от рассеяния пуль характеризуется столь узкими максимумами и минимумами, что никакой детектор их зарегистрировать не в состоянии. Расстояния между этими минимумами и максимумами неизмеримо меньше размеров самой пули. Так что детекторы будут давать усредненную картину, показанную сплошной кривой на рис. 1.
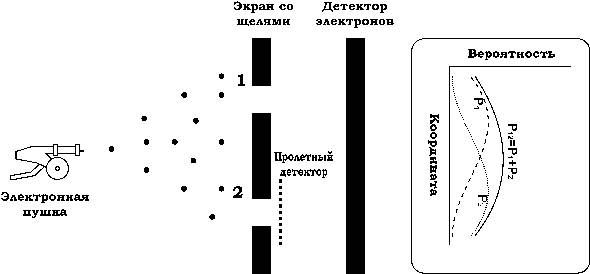
Давайте теперь внесем такие изменения в эксперимент, чтобы можно было "проследить" за электроном, то есть узнать, через какую щель он проходит. Поставим возле одной из щелей детектор, который регистрирует прохождение электрона сквозь нее (рис. 3).