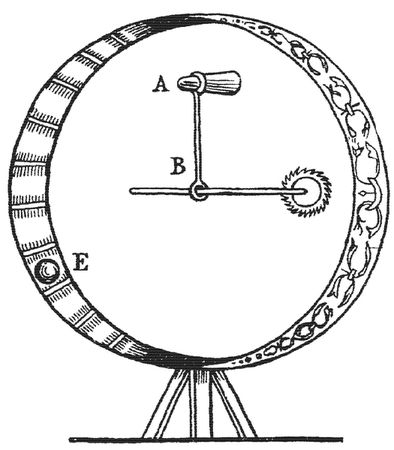
Таким образом, Уилкинс показал, что воздействие груза, вращающего колесо, определяется произведением силы (в данном случае - веса груза) на плечо (в данном случае - отрезок горизонтального радиуса до пересечения с вертикалью, проходящей через центр груза). Равенство всех таких произведений - моментов сил, действующих на колесо, обусловит его равновесие; неравенство - постоянное вращение. Остается только показать, что в любом из механических ppm такое равенство всегда соблюдается, и невозможность их действия доказана.
Уилкинс, правда, не ввел термина "момент силы", но от этого дело не меняется: важнейший закон статики был установлен. Работа Уилкинса помогла в дальнейшем механикам выдвинуть положения, которые вплотную подвели их к закону сохранения энергии и окончательно похоронили идею ppm-1. Но до этого было еще далеко.
Однако тучи над ppm сгущались не только со стороны теории. Неудачи с практической реализацией самых разных моделей тоже постепенно делали свое дело. Поэтому у некоторых (правда, очень немногих) изобретателей появлялось разочарование в идее ppm. Нашелся и достаточно мужественный человек, чтобы признаться не только самому себе, но и другим в бесполезности своей многолетней работы над такими машинами. Это был немец Иоганн Иоахим Бехер, который создал довольно сложный "физико-механический" ppm для привода часового механизма. Идея двигателя та же, что и других, описанных ранее, - движение перекатывающихся шаров - грузов, которые должны были приводить в движение систему взаимосвязанных шестерен и рычагов. Работа шла столь успешно, что курфюрст г. Майнца приказал воздвигнуть специальную каменную башню для размещения часов с двигателем Бехера. (Было это в 1660 г., почти в то же время, когда вышла книга Уилкинса.) Однако в дальнейшем это устройство не оправдало возлагавшихся на него надежд.
Бехер подвел итоги своей работы такими словами: "Десять лет я занимался этим безумием, потеряв кучу времени, денег и погубив свое доброе имя и славную репутацию - все это лишь для того, чтобы сегодня с полной убежденностью сказать: вечное движение - неосуществимо". Это признание осталось, к сожалению, неизвестным многочисленным изобретателям ppm.
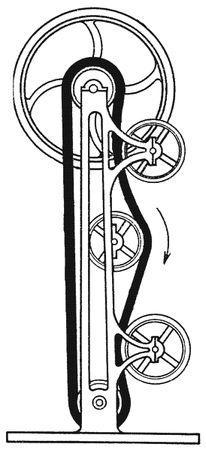
Вопрос о несостоятельности механических ppm с колесами и грузами был теоретически решен, хотя еще долгое время его понимание не стало общим достоянием. Но метод Уилкинса не мог непосредственно помочь при спорах о другом варианте механического ppm, например таком, который показан на рис. 1.12, где ремень (или цепь с грузами) с одной стороны тяжелее, чем с другой. Должна ли "работать" эта разница в весе или нет?
Теорию, которая позволила решить этот вопрос, разработал еще раньше замечательный голландский математик, механик и инженер Симон Стевин (1548-1620 гг.). Эта теория относится к равновесию тел, находящихся на наклонной плоскости, но выводы из нее имеют и более общее значение. Самое интересное в ходе рассуждений Стевина то, что он даже не считает необходимым доказывать невозможность создания ppm; он считает это истиной, не требующей доказательства, - аксиомой. Такую четкую позицию занимал до Стевина только Леонардо да Винчи.
Рисунок, относящийся к теории равновесия тел на наклонной плоскости, Стевин счел настолько важным, что вынес его на титульную страницу своего трактата "О равновесии тел", изданного в Лейдене (1586 г.). На рисунке Стевина (он воспроизведен на рис. 1.13) показана трехгранная призма, грани которой имеют разную ширину. Самая широкая грань установлена горизонтально, ниже других. Две другие, наклонные, сделаны так, что правая имеет ширину вдвое меньшую, чем левая. На призму накинута замкнутая цепь с 14 тяжелыми одинаковыми шарами. Рассматривая равновесие этой цепи, можно видеть (если исключить нижние восемь шаров, которые, очевидно, уравновешены), что на меньшей грани находятся два шара, а на большей - четыре. "Будет ли цепь находиться в равновесии?" - спрашивает Стевин. Если это так, то происходит чудо. Четыре шара уравновешиваются двумя!
"Не будь это так, - пишет он, - ряд шаров должен был бы (придя в движение) занять то же положение, что и раньше. По той же причине восемь левых шаров должны были бы, как более тяжелые, чем шесть правых, опускаться вниз, а шесть - подниматься вверх, так что шары совершали бы непрерывное и вечное движение".
Таким образом, возникает вопрос, ответ на который вынесен на надпись рисунка, помещенного на титульном листе: "Чудо не есть чудо" (на фламандском языке).

Стевин, исходя из невозможности вечного движения, утверждает, что никакого чуда нет и два шара совершенно "законно" уравновешивают четыре. Он выводит теорему: "Тело на наклонной плоскости удерживается в равновесии силой, которая действует в направлении наклонной плоскости и во столько меньше его веса, во сколько длина наклонной плоскости больше высоты ее".
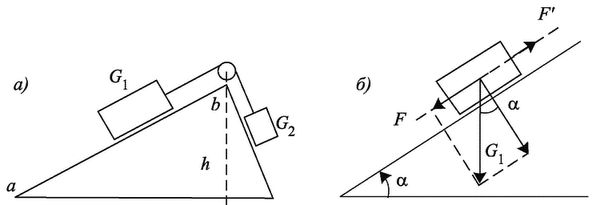
Если взять два груза G1 и G2 (рис. 1.14, а), то условие их равновесия для данных задачи Стевина запишется так:
G1 / G2 = ab / bc = 1/2.
Четыре шара весят как раз вдвое больше, чем два. Пользуясь современной терминологией, можно выразить эту теорему в более удобной форме (рис. 1.14, б): сила F’ удерживающая груз на наклонной плоскости и равная по значению противоположно направленной силе F, стремящейся его сдвинуть, определяется (если пренебречь трением) произведением его веса G на синус угла а наклона плоскости к горизонтали:
F = G sin α.
Если плоскость вертикальна, то α = 90° и sin α = 1, тогда F = G; если плоскость горизонтальна, то α = 0 и F = 0.
Стевин уверенно, опираясь на бесчисленные практические данные, вывел один из важнейших законов статики. Применяя этот закон к проектам ppm вроде показанного на рис. 1.12 и аналогичных ему, легко видеть, что вес наклонных частей тяжелого ремня (или грузов), висящих по диагонали, нельзя считать равным силе, с которой они поворачивают колеса двигателей. Нужно учитывать, что эта сила тем меньше, чем больше отклоняется ремень (или цепь с грузами) от вертикали. Если в каждом конкретном случае произвести соответствующий расчет, то выяснится, что силы, действующие с обеих сторон на колесо (или колеса) двигателя, будут неизбежно в точности одинаковы.
Таким образом, Уилкинс и Стевин создали научную базу, позволяющую показать нереализуемость любого механического ppm. Тем не менее отсутствие общей теории, показывающей неосуществимость любого ppm, оставляло возможности поиска как новых решений ppm, так и обоснований возможности его существования.
Это особенно чувствуется при ознакомлении с магнитными ppm. Наука о магнитах, в отличие от механики, была в самом зачаточном состоянии; поэтому и дискуссия вокруг них велась, главным образом, в общефилософском плане.
1.4. Магнитные ppm
Первым известным магнитным ppm была машина Петра Пилигрима (1269 г.), уже описанная в начале этой главы (рис. 1.4).
Новые виды магнитных вечных двигателей, появившиеся позже, основывались, так же как и первый, на аналогии между силой тяжести и силой притяжения магнита.
Такая аналогия была совершенно естественной, она подкреплялась общефилософскими соображениями; кроме того, силу притяжения магнита можно было непосредственно сравнить с силой тяжести.
Действительно, если на одну чашу весов положить кусок железа, а на другую - равную по весу гирю, то, воздействуя снизу на железо магнитом, можно определить его силу. Для этого нужно вновь уравновесить весы, добавочный груз будет равен силе притяжения магнита. Такое измерение произвел Николай Кребс (1401-1464 гг.), известный под именем Николая Кузанского (по селению Куза на Мозеле). Именно совместное действие двух тождественных сил - магнита и тяжести - служило идейной основой почти всех предложенных после Петра Пилигрима магнитных ppm.
Первым из них был двигатель, изобретенный Иоганном Теснериусом, Кельнским архиепископом конца 50-х годов XVI в. Он отдал много лет изучению всего, что связано с магнитами; это привело его к выводу, что "ни в одном случае вечное движение не достижимо никаким способом, кроме использования магнитного камня".
В сочинении о природе магнитных явлений он излагает своеобразную инструкцию для тех, кто пожелает сделать магнитный ppm, и приводит его схематическое изображение (рис. 1.15).