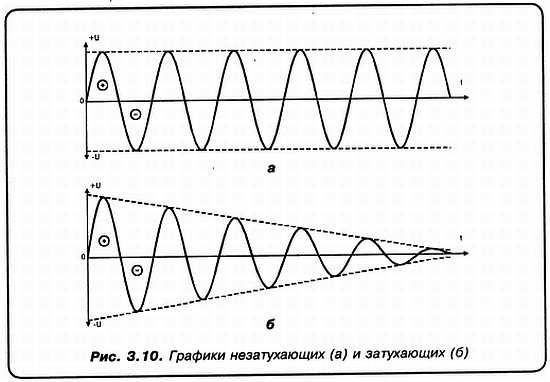
Так вот, численно, количество полных циклов заряд - разряд до, практически, полного затухания РАВНО ДОБРОТНОСТИ! Т. е. добротность Q = n, где n - количество полных циклов. А теперь от амплитудно-временных характеристик перейдем к АЧХ (рис. 3.11).
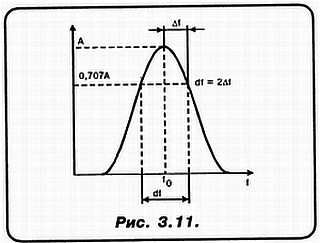
Вот эта, колоколообразная кривая (мы к ее рассмотрению вернемся в дальнейшем еще не раз) дает вторую, практически очень важную характеристику для Q:
Q = f0/2Δf,
где Δf - полоса пропускания по уровню 0,707.
И, кроме того, вот третья ипостась добротности, численно равная:
![]()
И если первая ипостась очень понятна, но не очень наглядна, поскольку кто успеет подсчитать точное число колебаний за очень малый промежуток времени, то вторая ипостась - может прямо выводиться на экран специальных анализаторов АЧХ! С ней удобно работать!
"Н": Ну, а третья?
"А": Третья ипостась - для реальных расчетов! Но любой колебательный контур характеризуется еще и частотой резонанса, или, что адекватно, частотой собственных колебаний:
![]()
Любопытно, что для получения одной и той же f0, можно взять различное соотношение L и С. Но формула для определения добротности показывает, каким именно должно быть соотношение L и С для получения требующейся нам ПОЛОСЫ ПРОПУСКАНИЯ КОЛЕБАТЕЛЬНОГО КОНТУРА! Она обозначена как df = 2Δf
"Н": А какого порядка эта величина должна быть?
"А": Смотря для чего! А вообще получение высоких добротностей - это сложная техническая задача! Но, в общем, вполне решаемая! Сейчас нам осталось рассмотреть еще одну важную физическую, а равно и техническую особенность колебательных контуров!
"Н": Ты снова рисуешь схему?
"А": А куда деваться (см. рис. 3.12)?
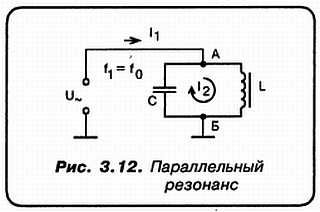
Здесь колебательный контур включен непосредственно в состав некоторой внешней цепи. Обрати внимание, Незнайкин, что в этом случае, когда частота внешнего генератора f1 совпадает с собственной частотой контура, последний представляет собой ЗНАЧИТЕЛЬНОЕ РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ для ВНЕШНЕЙ ЦЕПИ!
"Н": Но при этом ВНУТРИ контура LC реактивное сопротивление МАЛО!?
"А": Да, конечно!.. Дело в том, что за каждый период собственных колебаний контур LC теряет МАЛУЮ часть запасенной в нем энергии! Следовательно, этот контур будет потреблять из ВНЕШНЕЙ цепи ТОЛЬКО такую часть энергии, которая идет на компенсацию потерь за этот период! А это - очень незначительная величина! И она тем меньше, чем больше добротность контура Q!
"Н": То есть, если я верно понял, на резонансной частоте по отношению ко ВНЕШНЕЙ ЦЕПИ контур является БОЛЬШИМ СОПРОТИВЛЕНИЕМ, причем тем большим, чем больше его добротность?
"А": Абсолютно точно! Но есть и еще одно исключительно важное следствие! Не догадываешься, какое именно?
"Н": Может быть (см. рис. 3.12) что мы можем написать:
I2 = I1Q
Так или нет?
"А": Замечательно! Ну а что ты скажешь относительно напряжения?
"Н": У меня создалось впечатление, что напряжение на зажимах А и Б контура… может превысить напряжение генератора!
"А": И ты не ошибся! Оно превышает на частоте собственного резонанса подводимые извне колебания по амплитуде в Q раз!
"Н": То есть колебательный контур УСИЛИВАЕТ частоту, равную его резонансной в Q раз?
"А": Да! Но если во внешней цепи будут протекать токи, частоты которых не совпадают с резонансной, то они не создадут на зажимах контура сколько-нибудь заметного напряжения! Поэтому РЕЗОНАНСНЫЙ КОНТУР ОБЛАДАЕТ ЧАСТОТНОЙ ИЗБИРАТЕЛЬНОСТЬЮ!
"Н": Я уже дошел до кондиции, как того и хотел герой "Бриллиантовой руки". Всю впитанную (с кровью) информацию я должен осмыслить. В общем "принять ванну и выпить чашечку кофе"…
"А": Мы кое-что успели сегодня, дружище!
Глава 4. Устремленные в пространство
"Незнайкин": Наконец-то ты вновь удостоил меня аудиенции!..
"Аматор": О милорд, какой изысканный стиль! Ты случайно не перечитал "Трех мушкетеров", пока мы не виделись?
"Н": Ты почти угадал - "Одиссею капитана Блада"!
"А": Я так и понял по твоему высокому слогу! Кстати, я тоже очень уважаю книги о капитане Бладе! Но благородный и великолепный пират жил в буколическую эпоху! Когда медленное считалось быстрым!
"Н": Что ты хочешь сказать?
"А": В те времена новости из Америки в Европу шли, вернее плыли, месяцами! Скорость доставки информации была равна скорости хода каравеллы или галеона!..
"Н": В то время как сейчас для этого достаточно секунд!
"А": Долей секунды, дружище, долей секунды! И все благодаря свойствам… открытого колебательного контура!
"Н": Какого это - открытого? Простите, сэр! Следующий раз захвачу словарь, сэр!
"А": Хороший (в буколические времена говорили - добрый) учебник или пособие по радиотехнике помогло бы тебе больше! ОТКРЫТЫЙ КОНТУР - это просто техническое название для ПЕРЕДАЮЩЕЙ и ПРИЕМНОЙ антенн!
"Н": То есть мы сейчас вплотную подошли к вопросу о возникновении, распространении и возможности ПРИЕМА РАДИОВОЛН!?
"А": Да пора уж! Представь себе, что мы преобразовали колебательный контур таким образом, что он принял следующий вид (см. рис. 4.1).
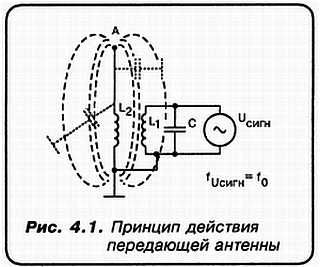
Здесь, фактически, мы имеем не один, а два колебательных контура. Первый - это контур, образованный С и L1, резонансная частота которого f0 равна частоте генератора Uсигн. Обмотки L1 и L2 связаны индуктивно. Поэтому во втором контуре также возникают колебания с частотой f0…
"Н": Относительно первого контура вопросов не имеется. Но вот где ты увидал второй контур? Я лично вижу только обмотку L2!
"А": Но ты не можешь не видеть, что верхний конец L2 переходит в некий проводник, который оканчивается точкой А?
"Н": Вижу… Но что дальше?
"А": А то, что это и есть второй, открытый колебательный контур! Его емкость является распределенной. То есть она образована как бы из множества малых емкостей между различными точками антенны и землей!
"Н": Выходит, что L2 входит в состав ЦЕПИ АНТЕННЫ?
"А": Ну конечно! А упомянутый уже вертикальный проводник - это ни что иное, как антенный штырь! Его длина может варьироваться в разных случаях от нескольких сантиметров до сотен метров! Да и само устройство антенны в реальности может быть исключительно сложным по своей конструкции!
"Н": Но если это и есть антенна, то она должна каким-то образом принимать близкие и далекие радиостанции. Разве нет?
"А": Верно! Однако в данном случае она не принимающая, а передающая. Попробуем представить себе, что при этом происходит… Видишь, на рис. 4.2 я изобразил только непосредственно антенну и то в очень упрощенном виде?