Квантовая теория информации таким образом непосредственно связывает информацию с энергией через энтропию фон Неймана, которую можно считать основной физической характеристикой энергоинформационного процесса. Изменение информации сопровождается изменением энергии, а обмен информацией напрямую связан с обменом энергией (справедливо и обратное) - это еще один важный вывод, который сделан в физике квантовой информации.
Есть и отдельные строгие результаты, связывающие информацию, энергию и энтропию. В частности, теорема Марголюса-Левитина утверждает, что число элементарных логических операций, которые физическая система может выполнить в единицу времени, ограничено энергией системы, а количество информации, которую система может зарегистрировать (воспринять), ограничено ее собственной максимальной энтропией.
Прямая связь между энергией и выполняемыми логическими операциями (информационными процессами) позволяет перекинуть мостик к физическим процессам, сопровождающим работу сознания, поскольку она непосредственно связана с логическими операциями.
Информация в терминах энтропии фон Неймана позволяет описывать запутанные состояния. Одна из основных особенностей этого понятия состоит в том, что об объекте, находящемся в чистом запутанном состоянии (ρ = ρ), невозможно получить никакой информации, поскольку в этом случае из (3.6) следует E(ρ) = 0. Энтропия фон Неймана и квантовая запутанность может быть отлична от нуля только для подсистем, которые взаимодействуют со своим окружением, и поэтому находятся в несепарабельном состоянии.
Довольно часто для простоты количество квантовой информации определяется просто как число кубитов в системе.
Исходная величина Tr(ρ) сейчас тоже широко используется в физике квантовой информации, но уже не в качестве меры информации, а как характеристика степени чистоты состояния (purity), которая показывает, насколько близко данное состояние к чистому, для последнего Tr(ρ) = 1.
3.5. Кубит и сфера Блоха
Кубиту в нашей книге отведена исключительно важная роль, поэтому вернемся к нему еще раз - теперь уже с привлечением матрицы плотности, которая помогает глубже понять, что такое кубит, и более подробно его описывает.
Пространство двух состояний, когда система может переходить из одного состояния в другое (двухуровневая система), является простейшим гильбертовым пространством. Когда система имеет одно состояние, и оно не меняется, то вообще не имеет смысла говорить о применении методов квантовой теории к такой системе и об описании ее в терминах состояний.
Если базисные векторы такого элементарного двухмерного пространства состояний обозначить |0ñи |1ñ, то в самом общем виде вектор состояния двухуровневой системы может быть записан в виде:
|Ψñ = a|0ñ + b|1ñ, (3.9)
где а и b - комплексные числа (амплитуды), удовлетворяющие условию нормировки |а| + |b| = 1.
Тогда, исходя из основных понятий квантовой механики, определение кубита звучит достаточно просто: кубит -это вектор состояния двухуровневой системы.
Таким образом, кубит- это минимально возможный (элементарный) вектор состояния. Любой вектор состояния может быть представлен как совокупность таких элементарных векторов, поэтому кубит - первооснова, исходный "кирпичик" для всех других векторов состояния любой размерности.
Подобно тому, как за единицу классической информации принимается бит (0 и 1), так в физике квантовой информации кубит определяется как единица квантовой информации.
Одним из сложных для восприятия квантовой механики моментов является отсутствие наглядных представлений, когда приходится иметь дело с векторами состояний и матрицами плотности. Как можно сопоставить вектор гильбертова пространства с привычными для нас трехмерными объектами? Один из наиболее простых вариантов такого сопоставления хорошо известен. Это так называемая сфера Блоха. Попытаемся разобраться, что она собой представляет.
В простейшем случае для системы, которая может находиться в двух состояниях (например, "вверх" и "вниз"), матрица плотности имеет размер 2 × 2 и для чистого состояния (3.9) она имеет вид:
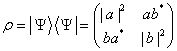. (3.10)
Существует и более общее выражение для матрицы плотности кубита, не только для того случая, когда он находится в чистом состоянии, как (3.10), но и для смешанного состояния, когда кубит взаимодействует со своим внешним окружением:
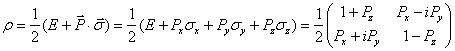, (3.11)
где Е - единичная матрица, 
= (Px, Py, Pz) - вектор Блоха (вектор поляризации), а 
= (σx, σy, σz) - вектор, компонентами которого являются матрицы Паули:
. (3.12)
Компоненты вектора Блоха определяются как средние значения матриц Паули по обычному правилу (3.8) Pj ≡ <σj> = Tr(ρσj); j = x, y, z.
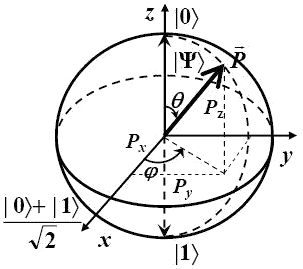
Три проекции вектора поляризации Px, Py, Pz, согласно (3.11), полностью определяют матрицу плотности кубита. В случае чистого состояния длина вектора поляризации равна 1, то есть 
, и этот вектор описывает сферу единичного радиуса, которая называется сферой Блоха (рис. 1). В этом случае компоненты вектора Блоха равны:
Px = sinθcosφ,
Py = sinθsinφ,
Pz = cosθ,
и два вещественных параметра (углы θ и φ) однозначно задают вектор состояния (матрицу плотности) кубита.
В случае смешанного состояния длина вектора поляризации становится меньше единицы, то есть 
, и он будет расположен внутри сферы.
Итак, матрица плотности кубита может быть представлена точкой в нашем привычном трехмерном пространстве. То есть существует взаимно однозначное соответствие между матрицей плотности и точкой шара единичного радиуса. Для чистого состояния (замкнутой системы) - это точка сферы.
