Ответ мы получим только для прямоугольного ящика. Для произвольного ящика выходит то же, только выкладки куда сложней. Нас еще будет интересовать ящик, размеры которого намного больше длины световых волн. В этом случае типов колебаний будет мириады и мириады; в каждом малом интервале частот Dw их окажется очень много, так что можно будет говорить об их "среднем числе" в каждом интервале Dw при частоте to. Начнем с того, что спросим себя, сколько типов колебаний бывает в одномерном случае - у волн в натянутой струне. Вы знаете, что каждый тип колебаний - это синусоида, кривая, обращающаяся на обоих концах в нуль; иначе говоря, на всей длине линии (фиг. 2.8) должно укладываться целое число полуволн.
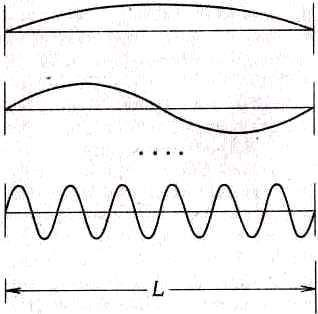
Фиг. 2.8. Типы стоячих волн на отрезке.
Мы предпочитаем пользоваться волновым числом k=2p/l; обозначая волновое число j-го типа колебаний через kj, получаем
где j - целое. Промежуток dk между последовательными типами равен
Нам удобно выбрать столь большое kL, что в малом интервале Dk; оказывается множество типов колебаний.
Обозначив число типов колебаний в интервале Dk через
, имеем
Физики-теоретики, занимающиеся квантовой механикой, обычно предпочитают говорить, что типов колебаний вдвое меньше; они пишут
И вот почему. Им обычно больше нравится мыслить на языке бегущих волн - идущих направо (с k положительными) и идущих налево (с k отрицательными). Но "тип колебаний", или "собственное колебание",- это стоячая волна, т. е. сумма двух волн, бегущих каждая в своем направлении. Иными словами, они считают, что каждая стоячая волна включает два различных фотонных "состояния". Поэтому если предпочесть под 
подразумевать число фотонных состояний с данным k (где теперь уже k может быть и положительным, и отрицательным), то тогда 
окажется вдвое меньше. (Все интегралы теперь нужно будет брать от k=-Ґ до k =+Ґ, и общее число состояний вплоть до любого заданного абсолютного значения k получится таким, как надо.) Конечно, стоячие волны мы тогда не сможем хорошо описывать, но подсчет типов колебаний будет идти согласованно.
Теперь наши результаты мы обобщим на три измерения. Стоячая волна в прямоугольном ящике должна обладать целым числом полуволн вдоль каждой оси. Случай двух измерений дан на фиг. 2.9.
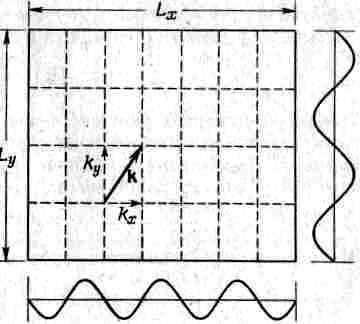
Фиг. 2.9. Типы стоячих волн в двух измерениях.
Каждое направление и частота волны описываются вектором волнового числа k. Его х-, у- и z-компоненты должны удовлетворять уравнениям типа (2.34). Стало быть, мы имеем
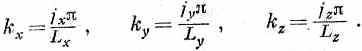
Число типов колебаний с kxв интервале Dkx, как и прежде, равно
то же и с Dky, и с Dkz. Если обозначить через 
(k) число таких типов колебаний, в которых векторное волновое число k обладает х-компонентой в интервале от kxдо kx+Dkx, у-компонентой в интервале от kyдо ky+Dky и z-компонентой в интервале от kzдо. kz +Dkz, то
Произведение Lx Ly Lz - это объем V ящика. Итак, мы пришли к важному результату, что для высоких частот (длин волн, меньших, чем габариты полости) число мод (типов колебаний) в полости пропорционально ее объему V и "объему в k-пространстве" DkхDkyDkz. Этот результат то и дело появляется то в одной, то в другой задаче, и его стоит запомнить:
Хоть мы этого и не доказали, результат не зависит от формы
ящика.
Теперь мы применим этот результат для того, чтобы найти число фотонных мод для фотонов с частотами в интервале Dw. Нас интересует всего-навсего энергия разных собственных колебаний, а не направления самих волн. Мы хотим знать число собственных колебаний в данном интервале частот. В вакууме величина k связана с частотой формулой
|k| =w/c. (2.39)
Значит, в интервал частот Dw попадают все моды, отвечающие векторам k, величина которых меняется от k до k+Dk независимо от направления. "Объем в k-пространстве" между k и k+Dk - это сферический слой, объем которого равен
4pkDk.
Количество собственных колебаний (мод) тогда равно
Однако раз нас интересуют частоты, то надо подставить k=w/c, и мы получаем
Но здесь возникает одно усложнение. Если мы говорим о собственных колебаниях электромагнитной волны, то каждому данному волновому вектору k может соответствовать любая из двух поляризаций (перпендикулярных друг другу). Поскольку эти собственные колебания независимы, то нужно (для света) удвоить их число. И мы имеем
Мы показали уже [см. (2.33)], что каждое собственное колебание (мода, тип колебаний, "состояние") обладает в среднем
энергией
Умножая это на число собственных колебаний, мы получаем энергию DЕ. которой обладают собственные колебания лежащие в интервале Dw
Это и есть закон для спектра частот излучения абсолютно черного тела, найденный нами уже однажды в гл. 41 (вып. 4). Спектр этот вычерчен на фиг. 2.10.