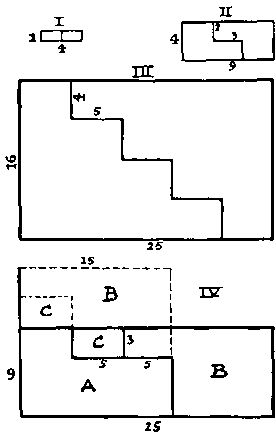
332. Прямоугольную доску можно разрезать методом лестницы на две части, из которых получится квадрат в том случае, если длины ее сторон совпадают с квадратами двух последовательных целых чисел. Так, в приведенной ниже таблице стороны соответственно равны 1 (или 1) и 2 (4), или 2 (4) и 3 (9), или 3 (9) и 4 (или 16) и т. д. Таблицу можно продолжать неограниченно.
| Стороны | Число | Сторона |
| ступенек | квадрата | |
| 1 × 4 | 1 | 2 |
| 4 × 9 | 1 | 2 |
| 9 × 16 | 1 | 2 |
| 16 × 25 | 1 | 2 |
| 25 × 36 | 1 | 2 |
На приведенном здесь рисунке случай I является простейшим - размер доски 1 × 4; в случае II доска имеет размер 4 × 9 и в случае III - 16 × 25. Можно заметить, что число ступенек увеличивается по определенному закону, а их размеры легко найти с помощью таблицы. Например, для доски 16 × 25, поскольку сторона квадрата равна 20, ступенька имеет высоту 20 - 16 = 4 и ширину 25 - 20 = 5.
Так как стороны выражаются квадратами, а произведение двух квадратов в свою очередь представляет собою квадрат, то площадь прямоугольника также выражается квадратом. Но отсюда вовсе не следует, что, например, доска размером 9 × 25 окажется подходящей, потому что ее площадь равна площади квадрата со стороной 15. На нашем рисунке в случае IV показан наилучший вариант для такой доски, но при этом доску приходится резать на три, а не на две части, как требуется. Это происходит потому, что ни число 9 не является кратным приросту высоты (6), ни число 25 - кратным убыванию длины (10). Следовательно, нужных ступенек здесь быть не может.
Конечно, подойдет любое кратное сторонам. Так, решение для случая 8 × 18 аналогично решению для случая 4 × 9 и содержит две ступеньки, при этом все размеры просто удваиваются. Доска 4 × 6¼ также подойдет нам, поскольку отношение ее сторон совпадает с отношением сторон у доски 16 × 25. Высота ступеньки будет равна 1, а ширина 1¼. В первом случае мы произвели сокращение, как у дроби, а во втором умножили все на 4, чтобы избавиться от дробей. Далее мы заметим, что и 4 × 9, и 16 × 25 являются квадратами последовательных целых чисел; следовательно, решение существует.
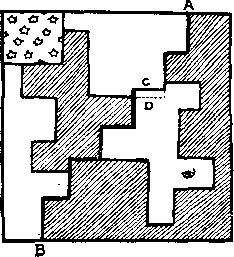
333. Несмотря на предупреждение, читатель мог предположить, что решением головоломки служит жирная зигзагообразная линия на нашем рисунке. Однако это не так, поскольку получившиеся части не совпадают по форме и размерам. Разрез следовало бы вести не по участку C, а по пунктирной линии D, но там отсутствует шов. На самом деле следует вырезать часть, которая заштрихована. Лоскут в левом верхнем углу показан для ориентации на исходном рисунке.
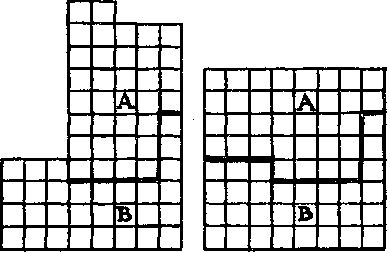
334. На рисунке показано, как следует разрезать линолеум на две части A и B, чтобы составить из них квадратную доску.
335. На рисунке слева показано, как можно покрыть квадрат 29 квадратными плитками, сохранив при этом 17 из них в целости и разрезав остальные 12 надвое. Части одной плитки обозначены одинаковыми цифрами.
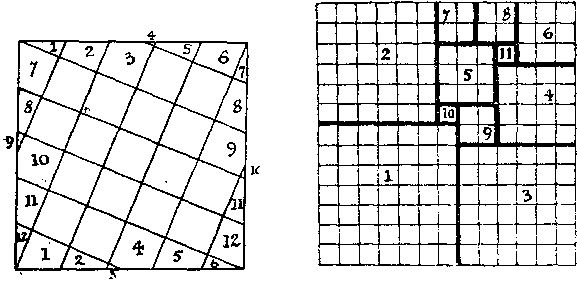
336. По-видимому, существует лишь одно решение этой головоломки, которое представлено на рисунке справа. Наименьшее число частей равно 11; они должны иметь указанные размеры. Три наибольшие части не могут располагаться иначе, а группу из восьми квадратов можно "отразить".
[По поводу общей задачи, так и не решенной до сих пор, о делении квадратного куска решетки любого размера вдоль ее линий на минимальное число меньших квадратов, см. гл. 15 книги М. Гарднера "Математические новеллы" (М., изд-во "Мир", 1974).
Насколько мне известно, соответствующая задача для треугольной решетки еще не рассматривалась. - М. Г.]

337. На рисунке показано, как разрезать квадрат на 4 части одинакового размера и одной формы так, чтобы в каждой из частей содержалось по звездочке и по крестику,
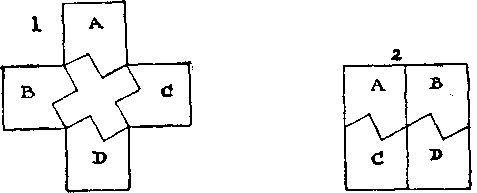
338. Если вырезать греческий крест меньших размеров (см. случай 1), то из четырех частей A, B, C и D можно сложить квадрат, показанный в случае 2.
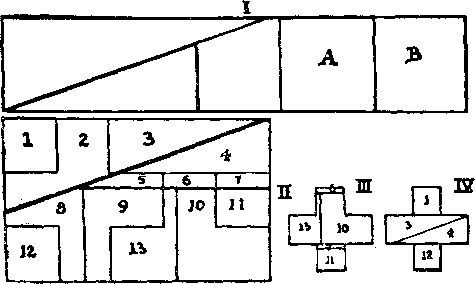
339. Отрежьте верхнюю и нижнюю части креста и поместите их в положения A и B (случай I), а оставшуюся большую часть разрежьте на 3 части так, чтобы из полученных 5 частей сложить прямоугольник, изображенный в случае II. Можно сказать, что этот прямоугольник составлен из 15 квадратов - по 5 квадратов на каждый новый крест. Остальные разрезы провести нетрудно. Из частей 2, 5, 8, 9 с очевидностью получается один крест; из частей 13, 6, 10, 7 и 11 - второй (случай III), а из 1, 3, 4, 12 получается третий крест (случай IV ). Площадь каждого конца малого креста составляет ⅓ площади любого конца большого креста.
(Число частей можно понизить до 12. - М. Г.]
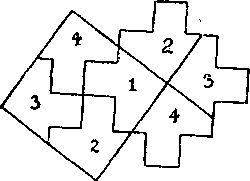
340. Как следует разрезать данную фигуру на 4 части, чтобы из них получился квадрат, показано на рисунке.
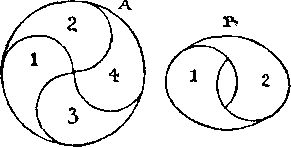
341. В случае A изображен круг, разделенный на 4 части, образующие "великую Монаду", а в случае B показано, как из двух таких частей можно составить один табурет (второй табурет получается аналогично из частей 3 и 4). Правда, отверстия для руки располагаются поперек, а не вдоль овалов, тем не менее все условия задачи выполнены.
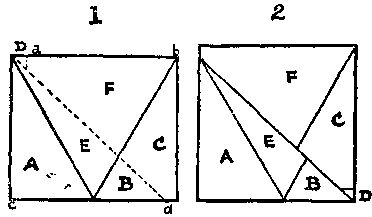
342. Разрежьте один из треугольников пополам и сложите части вместе, как показано в случае 1. Затем проведите разрез вдоль пунктирных линий так, чтобы и ab, и cd равнялись стороне искомого квадрата. Затем сложите полученные части вместе, как показано в случае 2, сдвинув F и C влево вверх и переместив маленький кусочек D из одного угла в другой.
[Существует решение данной задачи, содержащее только 5 частей. - М. Г.]
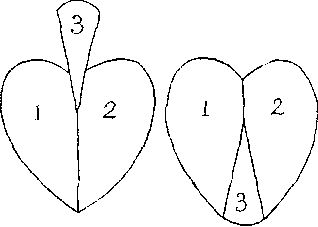
343. На рисунке показано, как можно разрезать символ масти пик на три части, чтобы получить символ червовой масти.
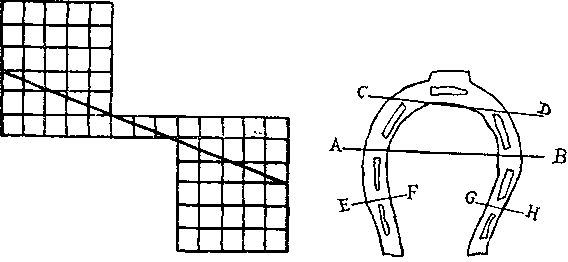
344. Вы видите на рисунке, как следует расположить 4 части, чтобы одна клетка исчезла (на первый взгляд). Объяснение этого феномена состоит в том, что края частей, расположенные вдоль жирной линии, не совпадают по направлению. Если вы расположите внешние края данной фигуры точно под прямым углом, то некоторые части перекроются и площадь перекрытой поверхности окажется равной площади одной клетки. Вот в чем и состоит простое объяснение нашего парадокса.
345. Прежде всего проведите разрез AB. Затем сложите полученные три части вместе так, чтобы при следующем взмахе ножниц вы могли провести одновременно разрезы CD, EF и GH (см. рисунок справа).
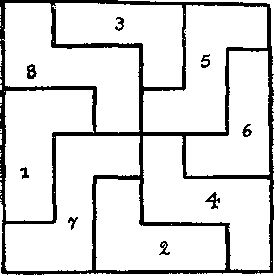
346. Восемь кусков фанеры можно расположить симметрично, чтобы они образовали квадрат таким образом, как показано на рисунке.
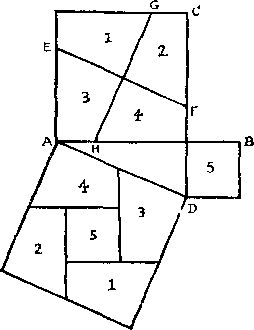
347. Сложите два квадрата вместе таким образом, чтобы линии AB и CD были прямыми. Затем найдите центр большего квадрата и проведите через него прямую EF, параллельную AD. Если вы теперь проведете через тот же центр перпендикулярно EF прямую GH, то больший квадрат разобьется на 4 части, из которых вместе с меньшим квадратом можно будет составить новый квадрат.
[Это решение было впервые найдено английским математиком-любителем Генри Перигейлом, который опубликовал его в 1873 г. Оно представляет собой одно из лучших доказательств теоремы Пифагора с помощью разрезания. См. гл. 38 книги М. Гарднера "Математические головоломки и развлечения" (М., изд-во "Мир", 1971). - М. Г.].