
В общем случае с помощью n прямых можно образовать (n - 3)(n - 1)(n + 1)/24 квадратов, если n нечетно, и (n - 2)n(n - 1)/24 квадратов, если n четно.
Если мы имеем m прямых, перпендикулярных другим n прямым, причем m меньше n, то число квадратов равно
![]()
257. Правило заключается в следующем. Если четыре стороны образуют арифметическую прогрессию, то наибольшая площадь равна квадратному корню из произведения всех сторон. Квадратный корень из 70 × 80 × 90 × 100 равен 7099 м. Это и есть верный ответ.
258. Площадь дорожки равна точно 66⅔ м, что станет совершенно очевидным, если вы представите себе маленький треугольный кусок, отрезанный снизу и перенесенный в правый верхний угол (см. рисунок).
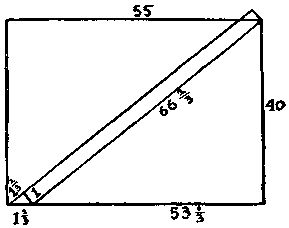
Докажем наше утверждение. Площадь всего сада равна 55 × 40 = 2200 м. Но (53⅓ × 40) + 66⅔ также равно 2200. Кроме того, сумма чисел ![]() и 40 должна равняться
и 40 должна равняться ![]() , что и выполняется в действительности.
, что и выполняется в действительности.
Общее решение таково. Обозначим ширину прямоугольника через B, длину через L, ширину дорожки через C и длину дорожки через x. Тогда
![]()
В нашем случае x = 66⅔; следовательно, основание прямоугольного треугольника с гипотенузой 66⅔ м и катетом, равным 40 м, составляет 53⅓ м.
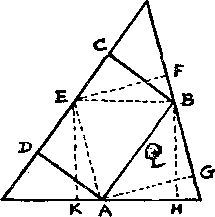
259. Разделим стороны треугольника точками A, B и E пополам. Если провести AB и опустить перпендикуляры DA и CB, то ABCD будет наибольшим возможным прямоугольником, а его площадь составит половину площади треугольника. Два других решения FEAG и KEBH подошли бы нам (у обоих та же самая площадь), если бы они не захватывали дерево. Это правило можно приложить к любому остроугольному треугольнику, а в случае прямоугольного треугольника получатся только два решения.
260. Многоугольник с произвольным числом сторон можно свести к равновеликому треугольнику, а поскольку угол AGF оказался прямым, то сделать это очень легко. Продолжим отрезок GA. Приложим линейку к точкам A и C, параллельно перенесем ее вверх до точки B и отметим точку 1. Затем соединим отрезком прямой точки 1 и D и параллельно перенесем его вверх до точки C, отметив точку 2. Теперь приложим линейку к точкам 2 и E, параллельно перенесем ее до точки D и отметим точку 3. Далее соединим линейкой точки 3 и F, параллельно перенесем ее до E, отметив точку 4. Если теперь мы соединим прямой точки 4 и F то получим треугольник G4F, площадь которого равна площади нашего неправильного поля. Поскольку на карте GF равно 7 см (70 м), то отрезок G4 равен 6 см (60 м) и площадь поля равна ½(70 × 60), или 2100 м. Этот простой и ценный способ определения площади многоугольников следовало бы знать каждому, но, увы, пока это остается лишь благим пожеланием.
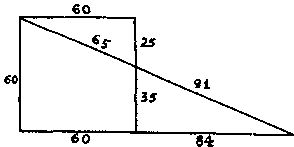
261. Все размеры приведены на рисунке. Обычно для того, чтобы найти решение, приходится решать биквадратное уравнение, но поскольку в условии задачи сказано, что ответ должен быть "в целых метрах", то можно заметить, что число 91 представимо в виде суммы квадратов единственным образом: 91 = 84 + 35. Зная это, определить все размеры очень легко. Искомое расстояние равно 35 м.
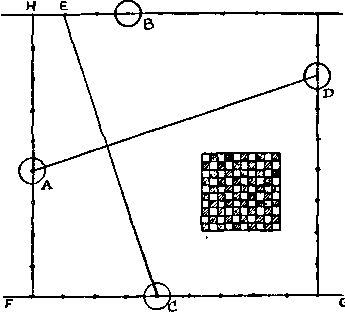
262. Соединим прямой точки A и D (см. рисунок) и построим отрезок CE, перпендикулярный и равный отрезку AD. Тогда точка E совпадет с центром одного из квадратов. Проведем прямую EB и продолжим ее в обе стороны. Проведем также через C прямую FG параллельно EB, а через A и D - перпендикуляры к EB и FG. Поскольку Н есть центр углового квадрата, то, приняв отрезок HE за единицу длины, мы обнаружим, что доска имеет размеры 10 × 10.
Если бы не были даны размеры шашек, то мы могли бы разбить доску на более мелкие квадраты. Но поскольку размеры шашек видны из рисунка, дальнейшее разбиение доски невозможно: в более мелких квадратах наши шашки просто не уместятся. Так как расстояние между центрами квадратов равно стороне квадрата, мы легко можем восстановить всю доску, что и показано на рисунке.
263. На рисунке слева показано чрезвычайно простое решение данной головоломки. Звездочка в центре - это офицер, а точки - солдаты.
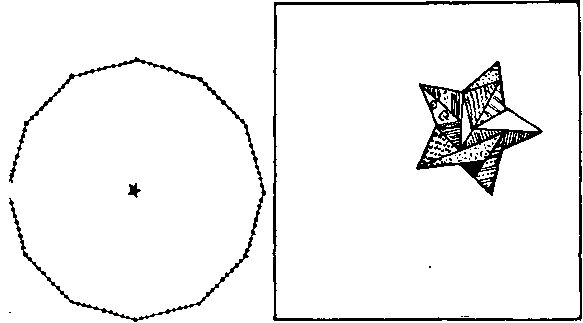
264. На рисунке справа изображена симметричная звезда в том самом положении, которое она занимает на скатерти. Все другие лоскутки для большей ясности не показаны. Удивительно, как трудно обнаружить звезду до тех пор, пока вам ее однажды не покажут. После эго решение становится совершенно очевидным.
265. Данную трапецию можно вписать в окружность. Полусумма x сторон равна 29. Вычитая из этого числа по очереди все стороны, мы получим 9, 13, 17, 19. Произведение этих чисел равно 37791. Квадратный корень из полученного числа равен 194,4, что и совпадает с размером искомой площади.
266. Продолжив приведенную ниже таблицу, вы сможете получить сколько угодно рациональных треугольников нужного вида.
| P | Q | Высота | Площадь |
| 2 | 4 | 3 | 6 |
| 8 | 14 | 12 | 84 |
| 30 | 52 | 45 | 1170 |
| 112 | 194 | 168 | 16 296 |
| 418 | 724 | 627 | 226 974 |
| 1560 | 2702 | 2340 | 3 161 340 |
Числа в таблице удовлетворяют соотношению 3P + 4 = Q. Каждое следующее значение P (начиная с третьего сверху) можно найти, умножив текущее значение P на 4, после чего следует вычесть из полученного произведения предыдущее значение P. Аналогично вычисляются и значения Q (начиная с четвертого сверху). Высота треугольника равна P/2, площадь - произведению высоты на Q/2. Длина средней из трех сторон всегда оказывается равной Q. В последней строке таблицы приведено наименьшее значение площади, делящееся на 20. Стороны треугольника в этом случае равны 2701, 2702, 2703, его высота 2340.
267. На приведенном здесь рисунке показано, как можно разделить окно на восемь просветов, "у которых все стороны тоже были бы равны". Каждый отрезок прута имеет равную длину.
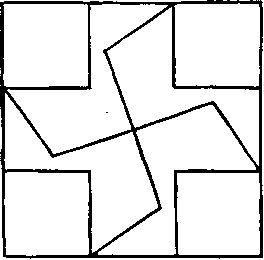
Подразумевалось (хотя явно и не оговаривалось), что площади всех просветов должны быть равными, а в нашем случае площадь каждого из четырех неправильных просветов на ¼ больше площади квадратного просвета и ни форма, ни число сторон у них не совпадают. И все же это решение точно удовлетворяет поставленным условиям. Если бы из каждой головоломки пришлось удалить все, что допускает неоднозначное толкование, то она оказалась бы перегруженной всевозможными условиями. Лучше оставить кое-что недоговоренным (разумеется, если речь идет не об олимпиадных задачах).
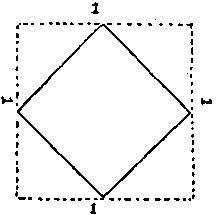
268. На рисунке пунктиром изображено первоначальное окно размером 1 м. После того как владелец загородил четыре угла, у него осталось квадратное окно вдвое меньшей площади, но в метр шириной и метр высотой.
269. Доску следует разрезать на расстоянии от В, равном 60![]() - 120 = 79,732...
- 120 = 79,732...