Умножив н. о. к. на 199, получим первое решение, умножив на 309 - второе, на 388 - третье и на 398 - четвертое решение. Выкладки можно существенно сократить, перескакивая через группы чисел, в которых цифры очевидным образом повторяются. Все ответы можно получить с помощью арифмометра за каких-нибудь двадцать минут.
118. Наименьшим возможным числом будет 3 333 377 733. Оно делится на 3 и на 7, и тем же свойством обладает сумма его цифр (42). Число должно содержать по крайней мере 3 семерки и 7 троек, причем семерки следует перенести как можно дальше вправо.
119. Искомыми числами являются 5832, 17 576 и 19 683. Сумма цифр каждого из них, равная соответственно 18, 26 и 27, совпадает с соответствующим кубическим корнем.
120. Наименьшее число, удовлетворяющее всем условиям, равно 35 641 667 749. Другие числа получаются прибавлением к данному любого целого, кратного числу 46 895 573 610.
121. Искомыми числами будут 162, 243, 324, 392, 405, 512, 605, 648, 810 и 972. Этим, по-видимому, исчерпываются все возможные случаи.
122. Существуют три решения: 56 169 (237), где 56 + 69 = 125 (5); 63 001 (251), где 63 + 01 = 64 (4) и 23 104 (152), где 23 + 04 = 27 (3).
123. Произведение чисел 989 010 989 и 123 456 789 равно 122 100 120 987 654 321, что и требовалось найти.
124. Ответ профессора гласил:
| 297 | 564 | 831 |
| 291 | 564 | 837 |
| 237 | 564 | 891 |
| 231 | 564 | 897 |
где разность прогрессии равна соответственно 267, 273, 327 и 333. Он указал на то, что для каждой из шести перестановок средних трех цифр можно найти соответствующее решение.
[В. Тебо в книге "Parmi les Nombres Curieux" показал, что существует 760 таких прогрессий. Кроме 456 и его перестановок, среднее число может быть любой перестановкой следующих групп из трех цифр: 258, 267, 348 и 357. - М. Г.]
125. Если вы умножите 6666 на сумму четырех заданных цифр, то получите правильный ответ. Поскольку 1, 2, 3, 4 в сумме дают 10, то, умножая 6666 на 10, получаем ответ 66 660. Если мы будем искать сумму всех выборок по четыре различные цифры, то получим 16 798 320, или 6666 × 2520.
126. Эту задачу можно решить несколькими способами. Ответ, разумеется, одинаковый во всех случаях, равен 201 599 999 798 400. Сумма девяти цифр равна 45 и
![]()
Записав далее
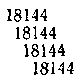
девять раз, сложив и приписав в конце 00, получим ответ.
127. С помощью четырех перестановок ![]() ,
, ![]() ,
, ![]() ,
, ![]() мы получим число 157 326 849, равное квадрату числа 12 543. Однако правильное решение -
мы получим число 157 326 849, равное квадрату числа 12 543. Однако правильное решение - ![]() ,
, ![]() ,
, ![]() - даст число 523 814 769, равное квадрату числа 22 887. При этом совершается всего три перестановки.
- даст число 523 814 769, равное квадрату числа 22 887. При этом совершается всего три перестановки.
128. Наименьший квадрат равен 1 026 753 849 (32043); наибольший - 9 814 072 356 (99066).
129. Задача имеет только два решения: числа 567 (567 = 321489) и 854 (854 = 729316). При поиске решения следует рассматривать лишь такие трехзначные числа, сумма цифр которых равна 9, 18 и 27 или 8, 17 и 26. Наименьшее трехзначное число, квадрат которого шестизначен, равно 317.
130. Суммы цифр данных шести чисел соответственно равны
| 46 | 31 | 42 | 34 | 25 | 34 |
| 1 | 4 | 6 | 7 | 7 | 7 |
Складывая цифры сумм (если потребуется - не один, а несколько раз), мы получим в результате однозначные числа, стоящие во втором ряду. Назовем эти однозначные числа цифровыми корнями исходных чисел. Цифровые корни можно объединить в группы из трех чисел восьмью различными способами
| 146 | 147 | 167 | 177 | 467 | 477 | 677 | 777 |
| 2 | 3 | 5 | 6 | 8 | 9 | 2 | 3 |
(Внизу выписаны цифровые корни.) Как показано в моей книге "Математические развлечения", цифровой корень квадрата должен равняться 1, 4, 7 или 9. Поэтому искомые числа должны иметь цифровые корни 4, 7, 7. Две семерки можно выбрать тремя способами. Но если бы пятое число содержалось среди искомых, то их сумма оканчивалась бы на 189 или на 389, что невозможно для квадрата, ибо в нем перед 89 должно стоять четное число или 0. Следовательно, ответ имеет вид
![]()
В правой части стоит число, равное квадрату 3645.
Чтобы подчеркнуть ценность этого нового метода, я позволю себе процитировать профессора Роуза Бола:
"Данное приложение целиком обязано своим появлением мистеру Дьюдени. Свойства цифр мало известны математикам, и мы надеемся, что его пример поможет привлечь внимание к этому методу... При решении некоторого класса арифметических задач метод цифрового корня оказывается чрезвычайно полезным".
131. 7 + 1 = 8; 9 - 6 = 3; 4 × 5 = 20.
132. Приведем пять решений задачи:
![]()
![]()
133. Цифры 4, 6 и 8 должны стоять во втором разряде, поскольку никакое простое число не может оканчиваться на эти цифры. Цифры 2 и 5 могут появиться в разряде единиц только в том случае, если простое число однозначно, то есть если нет других цифр. После этого решение без особого труда доводится до конца:
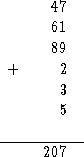
134. В каждом из следующих восьми примеров девять цифр используются по одному разу, а разность между соседними суммами равна 9.
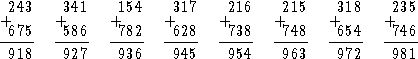
135. Число 94 857 312 при умножении на 6 дает 569 143 872, причем все девять цифр в каждом случае используются один и только один раз.
[Известны еще два решения: 89745321 × 6 = 538471926 и 98745231 × 6 = 592471386. - М. Г.]
136. Нетрудно представить число 24 с помощью трех четверок, пятерок, восьмерок или девяток:
![]()
![]()
![]()
Число 24 можно изобразить и с помощью трех единиц, шестерок и семерок. Действительно,
![]()
![]()