Предпринимались попытки уменьшить это время, но все они были основаны на трюках, так или иначе запрещенных. Например, Уокинхолма "вынуждали" оставлять не целый суточный рацион, а лишь его часть, совершать марш-бросок или съедать суточный рацион перед уходом с очередной отметки, чтобы он мог нести еще два суточных рациона и т. п. В последнем случае Уокинхолм на самом деле нес бы три рациона: один в желудке и два за плечами!
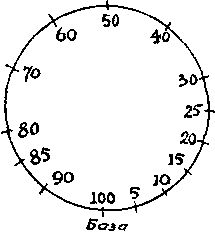
Если бы маршрут профессора пролегал по пустыне, то кратчайшее время равнялось бы 86 дням, а поступать следовало бы так.
Сложить 42 рациона в 10 милях от базы, вернуться на базу (42 дня). Отнести 1 рацион на отметку 15 миль, вернуться к первому складу в 10 милях от базы (1 день). Оставить 20 рационов в 20 милях от базы и вернуться к складу, расположенному в 10 милях от базы (20 дней). Отнести 1 рацион на расстояние 20 миль от базы и вернуться в точку, отстоящую на 15 миль от базы, взять ранее оставленный там 1 рацион и перенести его к отметке 20 миль (1 день). Перенести 10 рационов в точку, отстоящую на 30 миль от базы, и вернуться к отметке 20 миль (10 дней). Отнести 1 рацион к отметке 35 миль и вернуться к отметке 30 миль (1 день). Отнести 4 рациона на отметку 40 миль и вернуться к отметке 30 миль (4 дня). Отнести 1 рацион к отметке 40 миль и вернуться к отметке 35 миль. Взять там 1 рацион и перенести его к отметке 40 миль (1 день). Отнести 2 рациона в точку, отстоящую на 50 миль от базы, и вернуться к отметке 40 миль (2 дня). Отнести 1 рацион к отметке 55 миль и вернуться к отметке 50 миль (1 день). Перенести 1 рацион к отметке 60 миль и вернуться к отметке 55 миль. Взять там 1 рацион и перенести его на отметку 60 миль (1 день). Совершить оттуда переход до конечного пункта маршрута (2 дня). Всего - 86 дней.
77. Если человек, выйдя из A, пройдет 1⅔ км со скоростью 5 км/ч, то на это он затратит 20 мин. Обратный путь со скоростью 4 км/ч займет у приятелей 25 мин. Таким образом, человек догонит приятеля-инвалида в 12.35. Последний к тому времени проедет ⅔ км за 35 мин со скоростью 1
км/ч.
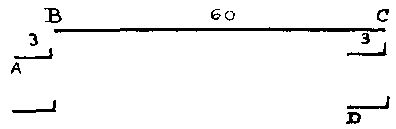
78. Предположим, что поезд идет в течение часа и имеет невероятную длину 3 км. Тогда (см. рисунок) за это время он пройдет от B до C 60 км, а пассажир переместится от A до C, или на 63 км. С другой стороны, если бы пассажир шел от паровоза в хвост поезда, то поезд успел бы пройти расстояние от B до C (снова 60 км), в то время как пассажир переместился бы лишь на расстояние от B до C, то есть на 57 км. Следовательно,в первом случае скорость пассажира относительно железнодорожного полотна составляет 63, а во втором - 57 км/ч.
79. Поскольку поезд идет 5 ч, разделим путь на 5 равных интервалов. Когда леди выезжает из Вюрцльтауна, 4 встречных поезда уже находятся в пути, а пятый лишь отправляется со станции. Каждый из этих 5 поездов она встретит. Когда леди проедет ⅕ пути, из Мадвилля отправится новый встречный поезд, когда она проедет ⅖ пути - еще один, ⅗ - еще один, ⅘ - еще один и, наконец, когда она прибудет в Мадвилль, оттуда как раз будет отправляться очередной, пятый, поезд. Если мы примем, как и следует сделать, что она не встречает "по пути" ни этот последний поезд, ни тот, который прибыл в Вюрцльтаун, когда ее поезд отправлялся оттуда, то по дороге из Вюрцльтауна в Мадвилль леди повстречает 9 поездов.
80. Слуга должен нести чемодан 1⅓ км и передать его джентльмену, который донесет чемодан до станции. Садовник должен нести другой чемодан 2⅔ км, а потом отдать его слуге, который и донесет чемодан до станции. Таким образом, каждый из них пронесет один чемодан 2⅔ км - иначе говоря, труд, который затратят на переноску багажа джентльмен, слуга и садовник, будет одинаковым.
81. Пусть n - число ступенек эскалатора; время, которое требуется, чтобы одна ступенька исчезла внизу, примем за единицу.
Тротмен проходит 75 ступенек за n - 75 единиц времени, или со скоростью 3 ступеньки за (n - 75)/25 единиц, времени. Следовательно, Уокер проходит 1 ступеньку за (n - 75)/25 единиц времени. Но он же проходит и 50 ступенек за n - 50 единиц времени, или 1 ступеньку за (n - 50)/50 единиц времени. Следовательно, (n - 50)/50 = (n - 75)/25, откуда n = 100.
82. Путешествие длилось 10
ч. Аткинс прошел пешком 5
км; Браун - 13
км, а ослик, принадлежавший Крэнби, пробежал в общей сложности 80
км. Надеюсь, ослику после такого подвига дали хорошенько отдохнуть.
83. Велосипедисты A, B, C, D могут проехать один километр соответственно за ⅙, 
, 
и 
ч. Следовательно, они совершают полный круг за 
, 
, 
и 
ч и, таким образом, в первый раз встречаются через 
ч (или, что то же, через 6⅔ мин). Четыре раза по 6⅔ мин составит 26⅔ мин. Поэтому четвертая встреча всех четырех велосипедистов произойдет в 12 ч 26 мин 40 с.
84. Брукс догонит Картера через 6⅔ мин.
85. 1) Муха встретит B в 1 ч 48 мин.
2) Определять расстояние, которое пролетит муха, не нужно. Это слишком трудная задача. Зато можно просто найти время, когда бы могли столкнуться автомобили, - 2 ч. На самом деле муха пролетает (в километрах):