Генри Дьюдени - Пятьсот двадцать головоломок стр 39.

47. Это бывает в 9 ч 6¾ мин, когда часовая стрелка проходит путь в 45 (6¾ в квадрате) минутного деления (после XII). Если бы мы допустили дроби, меньшие одной минуты, то нашлось бы еще одно решение, а именно: 12 ч 5 с ( мин).

48. Впервые это произойдет в 12 ч 5 мин, что можно будет неправильно истолковать (из-за идентичности стрелок) как 1 ч мин.

49. Если циферблат треснет так, как показано на рисунке, то сумма цифр в каждой из четырех частей будет равна 20. Искушенный читатель сразу заметит, что поскольку три десятки (римская цифра X имеется ввиду и в числах IX и XI) соседствуют друг с другом, то две из них должны быть объединены в одной части. Это можно сделать двумя способами.

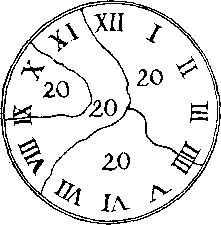
[В первом издании своих занимательных задач Дьюдени дал воистину дьявольское решение этой головоломки: IX надо было рассматривать вверх ногами и истолковывать как XI. (Именно так и делается на исходном рисунке.) Позже автор привел решение, показанное здесь. Существует еще двенадцать решений. Читателю предлагается самому отыскать их.

Предполагается, что римские цифры неподвижно прикреплены к ободку циферблата. Трещина может пересекать цифру, как показано на рисунке, но не может окружить какую-либо цифру, отделив ее от ободка. - М. Г.]

50. Вечер начался в 10 ч 59 мин, а когда гости посмотрели на стрелки, поменявшиеся местами, те показывали 11 ч 54 мин.

51. Истинное время равнялось 2 ч 5 мин.

52. В 3 ч 23 мин.

53. В 3 ч 41 мин.

54. Для того чтобы угол между стрелками был прямым, минутная стрелка должна быть точно на 15 мин впереди или сзади часовой. Каждое из этих положений встретится за 12 ч 11 раз, то есть через каждые 1 ч 5 мин. Если восемь таких промежутков времени пройдет после 9 ч, то часы будут показывать 5 ч 43 мин. С другой стороны, если после 3 ч пройдет два таких промежутка, то мы получим 5 ч 43 мин. Это и есть те два момента времени, которые требовалось найти в задаче, причем второй момент наступит, разумеется, раньше первого.

55. В 8 ч 23 мин и в 4 ч 41 мин. В головоломках с часами мы исходим из предположения, что на часах можно определить дробные доли минуты.

56. До вершины холма 6¾ км. Вверх Вилли-Лежебока взбирался 4½ ч, а вниз спустился за 1½ ч.

57. Поскольку человек проходит 27 шагов за то время, за которое автомобиль проезжает расстояние в 162 шага, ясно, что автомобиль движется в 6 раз быстрее человека. Человек движется со скоростью 3½ км/ч; следовательно, скорость автомобиля 21 км/ч.

58. Если бы каждый бегун, достигнув верхней площадки лестницы, сделал целое число полных шагов и неукороченный последний шаг, то наименьшим возможным числом ступенек было бы, конечно, 60 (3 × 4 × 5). Но из исходного рисунка видно, что у А, шагающего через 3 ступеньки, последний шаг будет длиной лишь в одну ступеньку. Б, перепрыгивающий через 4 ступеньки, на последнем шаге преодолеет всего лишь 3 ступеньки. И К, перепрыгивающему по 5 ступенек, на последнем шаге останется перескочить только через 4 ступеньки. Следовательно, нам надо найти наименьшее число, которое при делении на 3 дает в остатке 1, при делении на 4 дает 3 и при делении на 5 дает остаток, равный 4. Это число равно 19. Таким образом, лестница содержит 19 ступенек, из которых только 4 не изображены на рисунке.

59. Надо заметить (и в этом ключ к решению), что человек из Б. проходит 7 км за то же время, за которое человек из Э. проходит 5 км. Пусть, к примеру, расстояние между городами 24 км, тогда они встретились на расстоянии 14 км от Э. Человек из Э. двигался со скоростью 3 км/ч, а человек из Б. - со скоростью 4⅘ км/ч. Оба закончили свой путь в 7 час. вечера.

60. Велосипедист проедет один километр за 3 мин, или со скоростью км/мин. Ветер изменяет его скорость на км/мин. Следовательно, по ветру он движется со скоростью км/мин, а против ветра - со скоростью км/мин, так что 1 км он проезжает за 3 и за 4 мин соответственно, как и утверждалось.

61. За 3 мин. Команда в стоячей воде проходит ⅕ всего расстояния в минуту, а течение - всего расстояния в минуту. Разность и сумма этих дробей равны соответственно и . Следовательно, путь против течения займет (или 8) мин, а по течению (или 3) мин.

62. Если я прошагаю 26 ступенек; то мне потребуется на спуск 30 с, а если 34, то - 18 с. Умножая 30 на 34 и 26 на 18, мы получим 1020 и 468, разность между этими числами равна 552. Разделив ее на разность между 30 и 18 (то есть на 12), мы получаем в ответе 46, число ступенек на эскалаторе, который движется со скоростью 1 ступенька за 1½ с. Скорость, с которой я двигаюсь по эскалатору, роли не играет, поскольку ступенька, с которой я схожу, достигает платформы в один и тот же момент вне зависимости от того, что я делал до этого.

63. Пусть Андерсон проедет 11 км, бросит велосипед и оставшуюся часть пути пройдет пешком. Браун будет идти пешком до тех пор, пока не подберет велосипед, а затем проедет на нем оставшуюся часть пути. При этом он прибудет в пункт назначения одновременно с Андерсоном, и весь путь займет у них 3 ч 20 мин. Можно также разделить 20 км на 9 участков по 2 км каждый, причем Андерсон должен будет ехать первым. В этом случае Андерсон проедет каждый из своих 5 участков за ч и пройдет пешком каждый из оставшихся 4 участков за ч, затратив на весь путь 3⅓ ч. Браун проедет каждый из своих 4 участков за ч и пройдет пешком каждый из оставшихся 5 участков за ч, затратив на весь путь также 3⅓ ч. Расстояния, которые проедут Андерсон и Браун соответственно, относятся друг к другу как 5 к 4, а расстояния, которые они пройдут пешком, как 4 к 5.