![]()
Сколько времени займет отыскание этого произведения у читателя?
141. Интересный сомножитель. Какое число обладает тем свойством, что если его умножить на 1, 2, 3, 4, 5 или 6, то в ответе появятся лишь те цифры, которые содержатся в записи исходного числа?
142. Сумма кубов. Числа 407 и 370 совпадают с суммой кубов своих цифр. Так, 4 в кубе равно 64, куб 0 равен 0, а куб 7 есть 343. Сложив 64, 0 и 343, вы получите 407. Аналогично куб числа 3 (27), прибавленный к кубу числа 7 (343), даст 370.
Не могли бы вы найти число, не содержащее нуля и обладающее тем же свойством? Разумеется, мы исключаем тривиальный случай числа, равного 1.
143. Одинокая семерка.
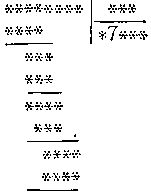
Эта головоломка, насколько я знаю, первый пример головоломки такого рода, в которой известна лишь одна цифра. По-видимому, она имеет единственное решение, и, как это ни странно, восстановить пропущенные цифры совсем нетрудно. Так, поскольку делитель, умноженный на 7, дает три цифры, то мы заключаем, что первая цифра делителя равна 1. Затем можно показать, что первая цифра делимого также равна 1. Поскольку две цифры делимого сносятся вниз, предпоследняя цифра частного равна 0. Наконец, первая и последняя цифры частного больше 7, поскольку в произведении с делителем они дают четыре цифры, и т. д.
144. Совсем без цифр.
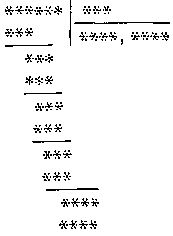
Вот головоломка, составленная мистером А. Корриганом, в которой не известно ни одной цифры. Обратите внимание на запятую в частном. Благодаря тому что после запятой стоят четыре цифры, головоломка решается неожиданно легко.
145. Простое умножение. Джордж Крэкхэм однажды за завтраком предложил следующую головоломку:

Джордж попросил поставить вместо звездочек все десять цифр в каждой строке так, чтобы при умножении получился правильный ответ. Он сказал также, что 0 не должен стоять ни в начале, ни в конце данных чисел.
Не сможет ли читатель найти ответ?
146. Полностью без цифр.
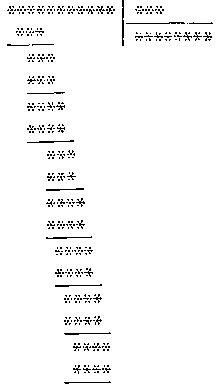
Вот еще одна хорошая головоломка. Условия ее таковы:
1. Никакая цифра не встречается дважды ни в одном ряду цифр, кроме делимого.
2. Если прибавить 2 к последней цифре частного, то получится предпоследняя цифра, а если 2 прибавить к третьей справа цифре частного, то получится четвертая справа цифра. Так, например, частное могло бы оканчиваться на 9742 или на 3186.
Нам удалось найти только одно решение.
147. Четные и нечетные.
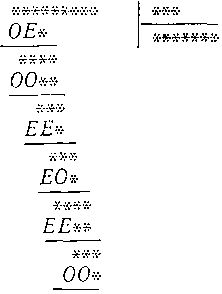
В этой головоломке с делением каждая звездочка и буква стоит вместо цифры, причем буква О соответствует нечетной (1, 3, 5, 7 или 9), а буква Е - четной (2, 4, 6, 8 или 0) цифре.
Не смогли бы вы восстановить все цифры? Задача допускает шесть решений. Быть может, вы сумеете найти одно из них или даже все.
148. Деление.
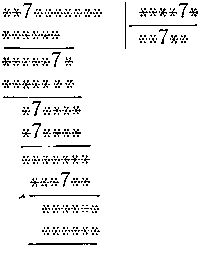
Не могли бы вы восстановить данный пример на деление, не стирая семерки и не заменяя их другими цифрами? Если вы попытаетесь решить задачу, считая, что все семерки заданы и других нет, то вы приметесь тем самым за явно безнадежную работу, хотя доказательство этого факта достаточно сложно. Задача решается сравнительно просто, если предположить, что любое число семерок разрешается ставить на любое место в промежуточных результатах (хотя вводить в делимое, делитель и частное другие семерки, кроме указанных в условии задачи, запрещается).
149. Без цифр.
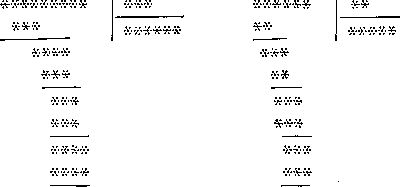
Следует помнить, что головоломки, в которых цифры заменены звездочками, нельзя решить, если нет дополнительных условий или не указано хотя бы одной цифры. Быть может, следующая головоломка близка к идеалу, хотя в ней производятся два деления, связанные между собой тем условием, что первое частное равно второму делимому. По-видимому, эта задача имеет лишь одно решение.
150. Действия с буквами. Существует много общего между теми головоломками, в которых следует восстановить арифметические действия по нескольким заданным цифрам и большому количеству звездочек, и теми, где каждая цифра заменена вполне определенной буквой, причем разным буквам соответствуют разные цифры. И те и другие головоломки решаются аналогично. Вот небольшой пример задач второго типа (вряд ли его можно назвать трудным):
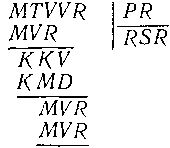
Можете ли вы восстановить это деление? Каждая цифра заменена своей буквой.
151. Арифметика букв. Вот головоломка с вычитанием, решение которой, возможно, доставит читателю несколько приятных минут.
Пусть АВ, умноженное на С, равно DE. Если DE вычесть из FG, то получится HI:

Каждая буква обозначает вполне определенную цифру (1, 2, 3, 4, 5, 6, 7, 8 или 9). Цифра 0 в записи примера не встречается.
152. Цифры вместо букв. Однажды утром профессор Рэкбрейн предложил своим юным друзьям следующую довольно трудную задачу. Он выписал буквы алфавита в следующем порядке:
![]()
- Каждая буква, - сказал он, - обозначает свою цифру от 1 до 9 (0 исключен). Четырехзначное число, умноженное на пятизначное, дает число, содержащее все 9 цифр в указанном порядке. Можете ли вы подставить цифры вместо букв так, чтобы выполнялось написанное равенство?
153. Тайна лавочника. Один лавочник, желая сохранить свои счета в тайне, выбрал слово из десяти букв (все разные) вроде ЗАЧЕРКНУТЬ, где каждая буква соответствует цифре в следующем порядке: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0. Например, в случае приведенного выше ключевого слова ЗА означает 12, ЧЕР - 345 и т, д. Если сумма записана в таком коде, то каким ключевым словом пользовался лавочник? Найти ответ нетрудно.
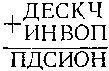
154. "Пчелиный воск". В неком секретном коде слово BEESWAX обозначает число. Полиция не могла найти ключ к этому коду до тех пор, пока среди бумаг не обнаружила следующую запись:
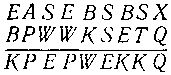
Сыщики предположили, что здесь изображена сумма, но никак не могли ее расшифровать. Затем одного из них осенила блестящая идея, что, быть может, здесь изображено не сложение, а вычитание. Догадка и в самом деле оказалась верной: подставив разные цифры вместо разных букв, сыщики разгадали код.
Какое число записывается в этом коде как BEESWAX?
155. От "неверного" к "верному".
- Из двух "неверно" не сделаешь "верно", - сказал кто-то за завтраком.
- Я в этом не уверен, - возразил полковник Крэкхэм. - Вот вам пример (каждая буква обозначает свою цифру, а все зашифрованные цифры отличны от нуля):

Если вы подставите нужные цифры, то равенство будет выполнено. Это можно сделать несколькими способами.
156. Умножение букв. В этом маленьком примере на умножение пять букв соответствуют пяти различным цифрам. Каким именно? Среди цифр нет нуля.
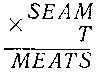
157. Секретный код. У двух конспираторов был секретный код. Иногда в их переписке попадались несложные арифметические действия, имевшие совершенно невинный вид. Однако в коде каждая из десяти цифр обозначала свою букву алфавита. Так, однажды встретилась сумма, которая, после того как вместо цифр подставили соответствующие буквы, приняла вид