1.3. Математическое моделирование атмосферных выбросов
В настоящее время усилиями ученых всего мира создан единый фонд моделей процессов, протекающих в живой и неживой природе. Эти модели, как правило, основываются на небольшом числе фундаментальных принципов, связывающих воедино разнообразные факты и представления естественных |наук. Каждая модель в этом фонде занимает определенное место, установлены пределы ее применимости и связь с другими моделями. Наличие такого фонда моделей придает уверенность исследователям при их использовании в практической деятельности - ведь каждая из этих моделей благодаря связям с другими моделями опирается не столько на специфическую проверку ее самой, сколько на весь практический опыт человечества. Для каждого конкретного объекта в этом фонде можно выбрать наиболее подходящую модель или модифицировать ее из близких по характеру моделей.
Применительно к задачам охраны окружающей среды развитость теорий возникновения и трансформации загрязняющих веществ в природных средах, проявившая себя в наличии грандиозного фонда природных процессов, с одной стороны, определяет высокую эффективность использования математических моделей и методов в инженерной практике, а с другой стороны - дает исследователям единую картину окружающего мира.
В целом основу конструктивного подхода к проблеме взаимодействия человека с природой дает моделирование (в частности, математическое) в сочетании с целенаправленными экспериментальными исследованиями. Загрязнение природных сред - одно из наиболее типичных проявлений такого взаимодействия.
Множество факторов, которое необходимо учитывать в моделях, находится на стыке ряда исследовательских программ [18-23], реализуемых в рамках наук о Земле. Комплексный характер подобных программ и наличие сложных прямых и обратных связей между гидрометеорологическими процессами, загрязнением природных сред, биосферой активно стимулируют разработки теоретических основ и системной организации математических моделей. На этом более высоком уровне системная организация оперирует с "простейшими" моделями как с элементарными объектами.
Применительно к математическому моделированию процессов возникновения и развития в атмосфере аварийных выбросов загрязняющих и токсичных веществ будем исходить из моделей физических процессов. К ним относятся модели гидротермодинамики атмосферы различных пространственно-временных масштабов, а также модели переноса и трансформации примесей, различные способы параметризации и т.п. В литературных источниках имеется достаточно много подобных разработок [21-23]. Их физический смысл и различия между ними зависят от конкретной постановки задач. В любом случае применительно к решению задачи методами численного моделирования исходят из понятий функций состояния и параметров.
Для удобства и краткости изложения воспользуемся операторной формой [19]. Обозначим векторную функцию состояния через
. К числу ее составляющих относятся поля гидрометеорологических элементов и концентраций загрязняющих примесей.
Вектор параметров обозначим
. Параметрами являются коэффициенты уравнений, параметры области интегрирования Dt сеточной области Dht , области размещения наблюдательных систем Dmt , начальные значения функций состояния, распределения и мощности источников тепла, влаги и других примесей и компонентов.
В операторном виде математическая модель описываемого процесса имеет следующий вид:
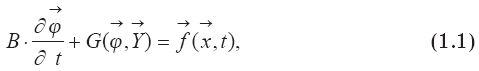
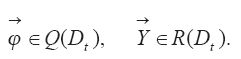
Здесь:
- нелинейный дифференциальный оператор матричной структуры, действующий на множествах функций
и
;
Q(Dt) - пространство функций состояния, удовлетворяющих граничным условиям;
R(Dt) - область допустимых значений параметров;
В - диагональная матрица, в которой все или часть элементов могут быть нулями;
- источники;
- , где D - область изменения пространственных переменных;
- интервал изменения времени t.
Входящий в соотношение (1.1) оператор
- определяется уравнениями гидротермодинамики системы атмосфера - почва - вода, переноса и трансформации примесей, а также условиями на границах раздела.
Граничные и начальные условия записываются для конкретного физического содержания модели.
В частности, для математической модели переноса примесей в атмосфере, которая входит в состав уравнения (1.1) в качестве составной части, получаем уравнение
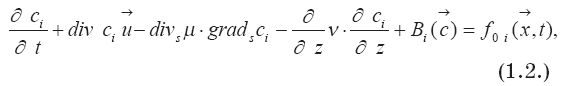
Эта модель учитывает процессы возможной трансформации веществ, турбулентного обмена и обменных процессов между природными средами: водой, воздухом и почвой.
В соотношении (1.2):
- концентрация примесей;
- вектор скорости с компонентами u,v,w в направлении пространственных координат
соответственно;
μ и ν - коэффициенты турбулентности в горизонтальных (x1,x2) и вертикальном (х3 = z) направлениях;
индексом s отмечены операторы, действующие в горизонтальных направлениях;
- операторы трансформации примесей;
- источники примесей (одновременно учитываются источники естественного и антропогенного происхождения).
Отметим, что операции с вектором
реализуются покомпонентно, т.е. уравнение (1.2) представляет собой систему n уравнений в частных производных. Оператор
- в общем случае нелинейный. Он определяет скорость изменения концентраций ci за счёт химических и фотохимических реакций. Скорости вертикального движения частиц (оседания или всплытия) учитываются функцией w. Примеси - многокомпонентны, количество компонент - входной параметр модели. На практике параметр модели определяется количеством химических веществ, участвующих в реакциях.
Модель дополняется начальными и граничными условиями: