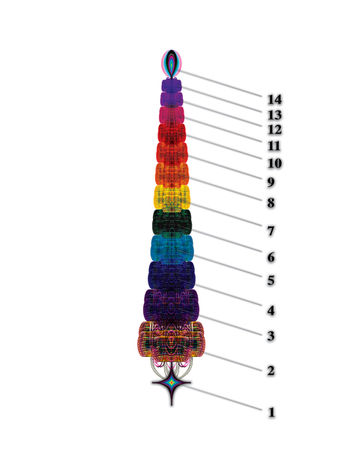
Эволюция этого процесса приводит к последовательному образованию вдоль общей оси систем метавселенных. Количество материй, образующих их, при этом, постепенно вырождается до двух. На концах этого "луча" образуются зоны где уже ни одна материя данного типа не может слиться с другой или другими, образовать метавселенные. В этих зонах возникает "продавливание" нашего матричного пространства и возникают зоны смыкания с другим матричным пространством. При этом, возможно вновь два варианта смыкания матричных пространств. В первом случае, смыкание происходит с матричным пространством с большим коэффициентом квантования мерности пространства и, через данную зону смыкания, могут притекать и расщепляться материи другого матричного пространства и возникнет синтез материй нашего типа. Во втором случае, смыкание происходит с матричным пространством с меньшим коэффициентом квантования мерности пространства - через данную зону смыкания, материи нашего матричного пространства начнут перетекать и расщепляться в другом матричном пространстве. В одном случае возникает аналог звезды супермасштабов, в другом - аналог "чёрной дыры" аналогичных габаритов.
Это отличие вариантов смыкания матричных пространств очень важно для понимания возникновения двух типов суперпространств шестого порядка - шестилучевика и антишестилучевика. Принципиальное отличие которых заключается лишь в направлении перетекания материй. В одном случае, материи из другого матричного пространства притекают через центральную зону смыкания матричных пространств и вытекают из нашего матричного пространства через зоны на концах "лучей". В антишестилучевике материи перетекают в противоположном направлении. Материи из нашего матричного пространства вытекают через центральную зону, а материи из другого матричного пространства втекают через "лучевые" зоны смыкания. Что же касается шестилучевика, то он образуется смыканием шести аналогичных "лучей" в одной центральной зоне. При этом, вокруг центра возникают зоны искривления мерности матричного пространства, в которых образуются метавселенные из четырнадцати форм материй, которые, в свою очередь, смыкаются и образуют замкнутую систему метавселенных, которая объединяет шесть лучей в одну общую систему - шестилучевик (Рис. 2.3.11).

Причём, количество "лучей" определяется тем, что в нашем матричном пространстве могут слиться, при образовании, максимально, четырнадцать форм материй данного типа. При этом, мерность возникшего объединения метавселенных равна π (π = 3,14...). Эта совокупная мерность близка к трём. Именно поэтому возникает шесть "лучей", именно поэтому говорят о трёх измерениях и т.д... Таким образом, в результате последовательного формирования пространственных структур, образуется балансная система распределения материй между нашим матричным пространством и другими. После завершения формирования Шестилучевика, устойчивое состояние которого возможно только лишь при тождестве между массой притекающих и вытекающих из него материй:
∫∫Ndmidi = 6 ∫∫ηdmidi (2.3.4)
где:
N - центральная область смыкания матричных пространств, через которую материи притекают в наше матричное пространство;
η - "лучевые" зоны смыкания с другим матричным пространством, через которое материи вытекают из нашего матричного пространства;
i - число форм материй, образующих шестилучевик;
mi - масса материй.
Тождество (2.3.4) для всего нашего матричного пространства можно записать в более удобном виде:
∫∫Ndmidi - 6 ∫∫ηdmidi= 0 (2.3.5)
Как видно из этой формулы, законы сохранения материи не нарушаются на любом уровне пространственных образований. От микрокосмоса до макрокосмоса они - общие. Единство законов которых следует, хотя бы уже из того, что микрокосмос является структурной базой макрокосмоса. У антишестилучевика циркуляция материи идёт в обратном направлении, от границ этого суперпространства к его центру. Причём, искривление матричного пространства - максимально в граничных областях и минимально в центре этого пространственного образования (Рис. 2.3.12).
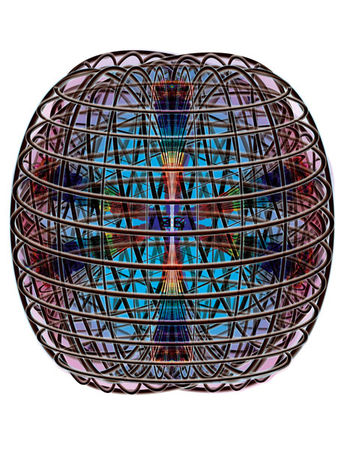
Условием устойчивого состояния антишестилучевика является гармония между вытекающими материями через центральную зону смыкания матричных пространств и синтезируемыми в граничных зонах смыкания (внешних) материями данного типа квантования мерности. Этот баланс можно описать тождеством вида:
∫∫Ndmidi = 6 ∫∫ηdmidi (2.3.6)
где:
N - центральная зона смыкания матричных пространств, через которую материи вытекают из нашего матричного пространства (супераналог - "чёрная дыра");
η - краевые зоны смыкания матричного пространства, через которые материи притекают в наше матричное пространство;
mi - масса материи данного вида.
Тождество (2.3.6) можно переписать в более удобном для понимания виде:
∫∫Ndmidi - 6 ∫∫ηdmidi = 0 (2.3.7)
Естественно, таких суперпространств в нашем матричном пространстве много. Они создают, как бы, узлы в матричном пространстве и являются "атомами" в нём. И вновь структура макрокосмоса аналогична структуре микрокосмоса. Это - ещё одно подтверждение их единства. Условием балансной устойчивости нашего матричного пространства является баланс между синтезируемой в матричном пространстве материей и материей вытекающей через зоны смыкания матричных пространств. Это условие можно записать в виде:
n1[∫∫Ndmidi - 6 ∫∫ηdmidi] ≡ n2 [∫∫Ndmidi - 6 ∫∫ηdmidi] (2.3.8)
где:
n1 - количество шестилучевиков;
n2 - количество антишестилучевиков;
N - центральная область смыкания матричных пространств, через которую материи притекaют в наше матричное пространство (шестилучевик);
N - центральная область смыкания матричных пространств, через которую материи вытекают из нашего матричного пространства;
η - лучевые зоны смыкания с другими матричными пространствами, через которые материи вытекают из нашего матричного пространства;
η - пограничные зоны смыкания с другими матричными пространствами через которые материи притекают в наше матричное пространство;
i - число форм материй;
m - масса материй.
Анализируя тождества (2.2.4, 2.3.6, 2.3.8), легко прийти к выводу о том, что они могут быть выполнимы только при условиях:
[∫∫Ndmidi - 6 ∫∫ηdmidi] ≡ 0
[∫∫Ndmidi - 6 ∫∫ηdmidi] ≡ 0 (2.3.9)
Это тождество отражает закон сохранения материи и определяет возможность устойчивого состояния Вселенной. И будет выполнимо только при условии баланса между притекающей и вытекающей из нашего матричного пространства материи, условие выполнения которого можно записать в виде:
∫∫Ndmidi - ∫∫Ndmidi ≡ 6∫∫ηdmidi - 6∫∫ηdmidi ≡ 0 (2.3.10)
Это тождество будет выполнимо, если:
∫∫Ndmidi - ∫∫Ndmidi ≡ 0
∫∫ηdmidi - ∫∫ηdmidi ≡ 0 (2.3.11)
или:
∫∫[Ndmidi - Ndmidi] ≡ 0
∫∫[ηdmidi - ηdmidi] ≡ 0 (2.3.12)
или:
∫∫[N - N]dmidi ≡ 0
∫∫[η - η]dmidi ≡ 0 (2.3.13)