"Кто же из нас прав?"
Все дети, наверное, умеют считать до десяти, может быть, и до двадцати и даже до ста. Это я уже по опыту знаю. Нет смысла проверять, как каждый из них станет говорить мне скороговорку, состоящую из "раз-два-три-четыре-пять" и т. д., произнесенную залпом, без запинки.
Нет смысла делать это сегодня, потому что дети пока никакого понятия не имеют о числе. Лучше начать с непривычных для них заданий, приводящих в движение уже накопленный ими опыт и придающих содержательный смысл этим скороговоркам "раз-два-три-четыре-пять…".
Но сначала надо выяснить, сколько фишек-слов было собрано в нашей коробке на уроке родного языка. Илико несет коробку, за ним идут Тенго и Майя.
- Их очень много! - говорит Майя.
- Больше ста! - поясняет Тенго.
Видите, сколько мы сегодня собрали слов! Завтра мы должны собрать еще больше! - говорю я, обращаясь к классу. - А вам большое спасибо, что помогли сосчитать фишки-слова!
- А зачем Вам нужно так много слов? - спрашивает Нато. Мне нужно?!
Я объясню это в следующий раз! - говорю я Нато. - А теперь приступим к уроку математики.
На первом уроке математики детям обычно разъясняют, что они начинают учиться считать, складывать и вычитать, делить и умножать. Предполагается, что это доступное для них объяснение предмета математики. Детям действительно понятно, когда им говорят: мы будем изучать, как отнять от пяти яблок три яблока, чтобы узнать, сколько останется; или же как прибавить к трем орешкам шесть орешков, как разделить десять груш на двоих и т. д. Но ведь не сложение и вычитание, не умножение и деление есть су!ъ предмета математики!
Пусть я допускаю методическую оплошность, но я поступлю вот так.
- Дети, вы знаете, что такое наука математика?
Тамрико. Это когда считаешь до ста… Елена. Надо считать до ста и еще уметь слагать… Я умею… К пяти прибавить пять будет десять…
Вахтанг. Я тоже умею складывать и вычитать… Папа учил…
Я подхожу к доске и приоткрываю занавеску. На ней цветными мелками написаны: формула Ньютона, формула производной функции, нарисована координатная система Декарта с функцией.
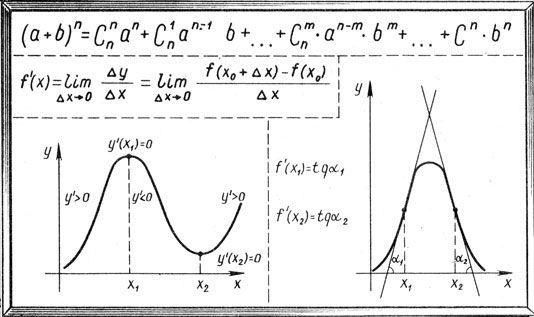
Формула Ньютона, формула производной функции, координатная система Декарта с функцией
Саша. Что это такое? Какие удивительные буквы! У детей широко раскрыты глаза, многие приподнялись с мест, чтобы разглядеть формулы получше.
- Это - настоящая математика, наука о количественных соотношениях и пространственных формах!
- Как красиво! - восклицает Лела, не отрывая глаз от доски.
- Потому что сама математика красивая. Ученые говорят - она царица наук.
Недоступно будет детям такое истолкование математики? Разумеется, мои дети не поняли много из того, что было сказано и показано мною. Но зато как было внушительно!
- Нравится вам математика?
- Да! - раздается восхищенно и единогласно.
Эка. Вы научите нас этому? (Указывает на формулы.)
- Я подготовлю вас к тому, чтобы вы научились понимать такие формулы. Хотите?
Опять восхищение и единогласное: "Да!"
- Так займемся этим делом!.. Садитесь прямо!.. Вот так!.. Посмотрите на эти фигуры и запомните их последовательность.
Я кладу у доски квадратики, на которых нарисованы фигуры:

Квадратики с фигурами
- Запомнили?.. Опустите головы!.. Закройте глаза… Поднимите головы… Скажите, что изменилось в последовательности фигур?
А последовательность теперь такая:
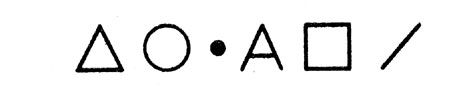
Квадратики с фигурами
Гига бежит к доске и кричит:
- Вы там переставили… вот это было здесь (показывает на точку), а буква А была здесь! - и он возвращает их на прежнее место.
- Запомните еще раз последовательность расположения фигур… Опустите головы и закройте глаза!.. Будете шептать мне на ухо, какие фигуры я переставил… Поднимите головы и посмотрите!
Перешептываясь с детьми, я обхожу класс. Ни одного правильного ответа! Я ведь ничего не менял в порядке фигур! В чем же дело? Сложная задача? Не может быть. По всей вероятности, мои доверчивые дети пока не могут представить, что я могу так пошутить с ними. Они ищут перестановки, которых на самом деле нет, но о которых я сказал.
- Дети, неужели вы не заметили, что я не трогал здесь ничего, что все фигуры остались на своих местах?
Майя. Я заметила, что там все так же, но не поверила…
Дато. Вы так действовали у доски, что я решил, что правда там что-то переставляете…
- В следующий раз будьте более внимательны. А теперь я. дам вам другое задание: вы должны определить, чего больше!
Перед детьми две доски. На перемене на них я нарисовал следующего рода множества для заданий: сколько, чего больше, из чего, где больше (справа, слева, внизу, наверху). Все это - на первой доске. На другой же разбросаны фигуры по всей площади. Детям надо будет выяснить, "сколько чего". Приоткрываю одну треть первой доски.

На доске нарисован род множеств для заданий
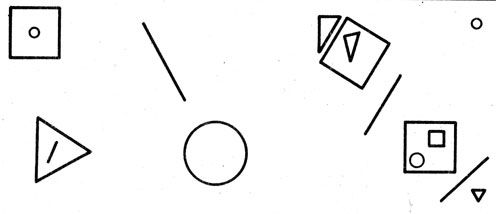
На доске нарисован род множеств для заданий
- Скажите, пожалуйста: сколько здесь кружков?
- Пять! - говорят дети.
- Кто может сказать, какая из них цифра пять? - Я показываю карточки с цифрами от нуля до девяти.
- Вот эта, которая в середине! - отвечают многие.
- Вот эта? - беру цифру 3.
- Нет! Которая была рядом!
- Ага, значит, вот эта! - Я достаю цифру 4.
- Нет, - говорит Майя, - вы ошиблись, не ту цифру взяли… Можно, я вам покажу?
- Покажи, пожалуйста!
Майя выбегает, достает из колоды цифру 5.
- Какая это цифра, дети? - показываю всем.
- 5! - отвечают они.
- Спасибо, Майя!
Вместо цифры 4 я кладу на доску цифру 5. Теперь все в порядке.
- Сколько здесь треугольников? - я обвожу указкой группу треугольников.
- Четыре… Четыре! - отвечают они вразнобой.
- А какая из этих цифр - 4? Эта? - показываю им цифру 2.
- Нет… Это 2!
- Может быть, эта? - показываю цифру 6.
- Нет… Это 6!
- Так значит, вот эта?
- Нет… Это 7!
Дети развеселились. Им не терпится показать мне 4. Магда выбегает (разумеется, без разрешения), дотягивается до моей руки и показывает на карточку с цифрой 4.
- Вот это - цифра 4!
- Спасибо, Магда, что помогла найти цифру 4. А сколько здесь квадратиков?
- Шесть! - получаю ответ. Беру из колоды цифру 6 и ставлю в перевернутом виде рядом с предыдущими цифрами. Дети весело подсказывают:
- Так получается девять, надо перевернуть… тогда и будет шесть!
Я принимаю замечание.
- А там семь! - выкрикивает Котэ и показывает на группу прямых.
- Котэ говорит, что здесь семь прямых, а я думаю, что восемь! Кто же из нас прав?
- Вы! - кричат многие, не задумываясь.
- Он! - говорят очень немногие, указывая на Котэ.
А Майя сосредоточилась, внимательно смотрит на доску и шепчет. Вот она встает с места:
- Можно, я скажу?.. Там семь прямых линий, а не восемь, и потому прав этот мальчик, а не Вы!
- Согласны с Майей?
Моих сторонников стало меньше. Элла встает, быстро подходит к доске и считает про себя прямые.
- В чем дело, Элла?
- Семь линий, а не восемь! - говорит она и бежит обратно к своей парте.
- Сосчитаем, пожалуйста, все вместе!
Я указкой показываю сначала на одну, затем на другую прямую.
- Одна… Две… Три! - считают дети хором. Подольше задерживаю указку на четвертой прямой.
- Четыре… Пять! - продолжают они, не дождавшись перемещения кончика указки. Майя протестует: все перепуталось и так считать нельзя. Начинаем снова. Теперь уже в быстром темпе движется моя указка и, получив хоровое "семь", начинаю снова касаться кончиком указки тех же прямых.
- Восемь… Девять… Десять… Одиннадцать!..
Но голоса постепенно слабеют, многие вдруг понимают, что опять все запуталось. Я вызываю к доске Майю помочь нам сосчитать прямые. Третье хоровое чтение - с помощью Майи - проходит успешно.
- Ну, конечно, семь, а не восемь. Котэ прав! - говорю я и ставлю цифру 7 на доску рядом с другими цифрами. Дети внимательно следят, не ошибусь ли я. Кто-то все же выкрикнул: "Это не семь!" Но другие подтвердили, что это именно семь, а не другая цифра.
- А теперь посмотрите на группу этих точек. Сосчитайте, пожалуйста, сколько их здесь, и шепните мне на ухо!
Быстро подхожу к каждому, кто меня призывает. И на меня сыплются ответы, нарушающие все устои точности математической науки: "Пять… Девять… Десять… Двадцать… Сто… Тысяча… Миллион!". A Tea шепчет мне, что там очень много точек и их невозможно сосчитать. Я останавливаюсь у ее парты.
- Tea, повтори, пожалуйста, погромче, чтобы слышали все: сколько там точек?
- Точек очень много, их трудно сосчитать!
- Спасибо, Tea!.. А вы как думаете?..