9.33. Наряду с решением (x1, у1) система имеет решение (x1, −у1). Она может иметь единственное решение лишь при у = 0. Подставив это значение у, находим, что а = 0. Достаточно ли выполнение условия а = 0 для того, чтобы у системы было единственное решение?
9.34. После исключения ![]() получится уравнение
получится уравнение
/y² − 2/y + у² + 2x − 2у = 3.
Его не следует преобразовывать в уравнение четвертой степени. Если в качестве вспомогательного неизвестного z взять некоторое выражение, содержащее x и у, то получится квадратное уравнение относительно z.
9.35. Все прямые у = а(x + 5) + 4 проходят через точку (−5; 4). Построение графика функции у = |6 − |x − 3| − |x + 1|| удобно начать с построения графика функции
у = 6 − |x − 3| − |x + 1|.
9.36. Уравнение равносильно системе
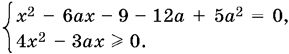
У первого уравнения есть корни
![]()
Остается выяснить, когда их два, а когда один, а также, при каких а для каждого из них удовлетворяется участвующее в системе неравенство.
9.37. Для упрощения симметрических многочленов применяют подстановку x + /x = t. Здесь возможна похожая подстановка. Наличие в числителе каждой дроби множителя x упрощает решение.
9.38. Вы упростите вычисления, если обратите внимание, что 84 693 делится на 327.
K главе 10
10.1. Ввести обозначения а = 1 + k и b = 1 − k.
10.2. Обозначим выражение, стоящее в левой части неравенства, через P. Разделив его на а1а2...аn = 1, после несложных преобразований получим
![]()
Для оценки P удобно рассмотреть теперь Р² и заметить, что
![]()
10.3. Способ 1. Воспользоваться тем, что с > а и с > b, и оценить каждое слагаемое.
Способ 2. Применить свойство показательной функции, приняв во внимание, что а < с, b < с.
10.5. Использовать условие а + b + с = 1, чтобы убедиться, что неравенство будет обязательно строгим.
10.7. Показательная функция (/b) , в силу условия задачи, является возрастающей.
10.8. Применить неравенство между средним арифметическим и средним геометрическим к произведению каждых двух чисел, равноотстоящих от концов в выражении n!.
10.9. Способ 1. В неравенстве (1 − u)(v − 1) > 0 (см. указание I на с. 141) раскрыть скобки и воспользоваться неравенством между средним арифметическим и средним геометрическим чисел uv и w.
Способ 2. Воспользоваться неравенством /v + /u > 2 (сложить его с полученным в указании I).
10.10. Оценить произведение (p − а)(p − b)(p − с) суммой этих чисел можно, воспользовавшись неравенством
xyz ≤ /27 .
10.12. Зная выражения у + z и уz через x, можно записать квадратное уравнение с коэффициентами, зависящими от x, корнями которого будут у и z.
10.13. Выразив у + z и уz через x, придем к квадратному уравнению, коэффициенты которого зависят от x. Поскольку в условии сказано, что x, у и z - действительные числа, дискриминант полученного уравнения не должен быть отрицательным. (!!)
Найденные границы изменения x, в силу симметрии данных уравнений, распространяются на у и z.
10.15. Чтобы данный трехчлен был отрицательным внутри некоторого отрезка, необходимо и достаточно, чтобы на концах отрезка он принимал неположительные значения.
10.16. Доказать, что условие а > 0 несовместно с требованием, в силу которого оба корня больше а.
10.17. Так как k ≠ 0 (иначе условие задачи неосуществимо), то парабола должна иметь один корень в интервале (−1, +1), а другой вне этого интервала.
Такое расположение параболы имеет место тогда и только тогда, когда значения трехчлена в точках −1 и 1 противоположны по знаку.
10.18. Если ветви параболы будут направлены вверх и, кроме того, парабола не будет пересекать положительную полуось Оx, то мы получим расположение параболы, необходимое и достаточное для выполнения условия задачи.
10.22. Числитель и знаменатель полученной дроби должны иметь разные знаки. Приходим к совокупности двух систем.
10.23. Неотрицательный множитель можно отбросить, исключив точки, в которых он обращается в нуль. Оставшееся неравенство удобно привести к виду, в котором правая и левая части неотрицательны, и возвести в квадрат с учетом соответствующих ограничений.
10.24. При x > 0 данное неравенство можно возвести в квадрат (учтя соответствующие ограничения), так как обе его части положительны. При x < 0 неравенство исследуется аналогично.
10.25. Составить квадратное неравенство относительно