K главе 5
5.2. В треугольнике АМВ рассмотреть медиану, выразить ее квадрат через стороны треугольника, воспользоваться полученными ранее соотношениями. (!!)
Доказать, что медиана МС равна AB.
5.3. Косинус угла А, участвующий в теореме косинусов, можно определить из треугольника АМО, где О - центр окружности, о которой идет речь в условии задачи. (!!)
Обратное утверждение можно доказывать в такой форме: если AC = 2ВС и 2АМ² + МВ² = АВ², то АО = МО. Здесь тоже естественно воспользоваться теоремой косинусов для треугольника АМВ. Единственное осложнение возникает из-за необходимости выразить cos А через линейные элементы. Можно поступить иначе: записать теорему косинусов для треугольника АМО, имеющего с АМВ общий угол А, и исключить cos А.
5.4. Два треугольника АМВ и ВМС, имеющие общую сторону ВМ, равновелики тогда и только тогда, если их высоты, опущенные из вершин А и С на общую сторону ВМ, равны.
Задача свелась к построению прямой, проходящей через точку В и равноудаленной от двух данных точек А и С. (!!)
Существуют две и только две прямые, проходящие через точку В и равноудаленные от точек А и С: одна - параллельная AC, другая проходит через середину AC.
5.5. Если прямые AB и CD пересекаются в точке N, то отрезки AB и CD следует перенести в эту точку, двигая каждый по своей прямой. После этого задача сведется к предыдущей (см. задачу 5.4). (!!)
Если прямые AB и CD параллельны, то отрезки AB и CD удобно расположить так, чтобы их центры лежали на общем перпендикуляре. Этот перпендикуляр остается разделить в отношении CD : AB.
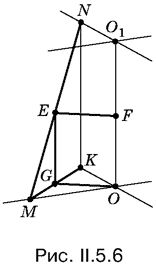
5.6. Пусть MN - отрезок длины l, E - его середина, а длина отрезка ОО1 равна а (рис. II.5.6). Если спроецировать точку E на плоскость нижнего основания, то легко вычислить длину отрезка GO, равного отрезку EF. (!!)
Поскольку длина отрезка GO, равного отрезку EF, не зависит от расположения отрезка MN, то точка E лежит на окружности радиуса EF с центром в точке F. Остается установить обратное предположение и вспомнить о том, что отрезок не должен находиться вне куба.
K главе 6
6.1. Воспользоваться тем, что p − 1, p, p + 1 - три последовательных числа, причем p - простое, большее трех.
6.3. Если n = 2k + 1, то а + b = (а + b)(а − ... + b).
6.4. Среди этих же чисел будет /2 = 62, делящихся на 8 = 2³ и т. д.
6.5. Так как сумма цифр числа делится на 81, то естественно предположить, что оно делится на 81. Однако такой признак делимости не был доказан в курсе арифметики, и поэтому придется дважды воспользоваться признаком делимости на 9. Для этого удобно разбить цифры числа на 9 групп, каждая из которых делится на 9.
6.6. Если многочлен n + 4 разложен на множители второй степени, то он может быть простым числом только в том случае, если один из множителей равен единице.
6.7. Чтобы убедиться, что числитель всегда делится на число, стоящее в знаменателе, его придется разложить на множители.
6.8. Способ 1. Предположим, что данная дробь сократима. Тогда 5x + 7 = qr, 2x + 3 = pr. Рассматривая эти равенства как систему уравнений относительно x, исключим x.
Способ 2. Рассмотреть вместо данной дроби обратную и выделить целую часть.
6.10. Пример дальнейших рассуждений: при умножении цифры с на 3 мы должны получить число, оканчивающееся на 1. Это возможно лишь при с = 7.
6.11. Так как p - число нечетное, то мы имеем три последовательно нечетных числа. Докажите, что одно из них обязательно делится на 3.
6.12. Если tg 5° - рациональное число, то cos 10° и cos 30° - тоже рациональные числа.
6.13. Сумма девяток должна быть на 10, или на 21, или на 32, или на 43, ... меньше числа, которое делится на 11. Чему должны быть равны в сумме остальные цифры?
6.14. Однородные выражения удобно преобразовывать с помощью замены у = kx. Так как x и у - целые числа, то число k - рациональное, т. е. k = /q . Остается рассмотреть возможные значения сомножителей, произведение которых равно 17. Нужно добиться того, чтобы каждый сомножитель был целым числом.
6.15. Удобно записать уравнение в виде (x − 2у)(x + 2у) = 5² · 9 · 89 и вспомнить, что мы ищем целочисленные решения.
6.16. Условие 11(4x − 1) = 69(у − x) удовлетворяется при целочисленных значениях x и у, только если 4x − 1 = 69k, у − x = 11n. Из первого соотношения следует, что k + 1 делится на 4. Отсюда k = 3, 7, 11, ... .
K главе 7
7.1. Вынести за скобки в числителе ![]() , а в знаменателе
, а в знаменателе ![]() . После этого дробь сократится.
. После этого дробь сократится.
7.2. Трехчлен 1 + x − x² является общим множителем знаменателей дробей в первой скобке.
7.3. Последнее слагаемое нужно преобразовать отдельно, после чего его можно будет объединить с первыми двумя.
7.4. Поскольку степень каждого члена числителя вдвое больше степени соответствующего члена знаменателя, то дробь целесообразно умножить на выражение, сопряженное знаменателю.
7.6. Преобразовать подкоренные выражения, прибавив и вычтя из них единицу. При извлечении корня использовать условия задачи.
7.7. Можно воспользоваться формулой сложного радикала