![]()
после чего коэффициенты при sin α и cos α можно объявить косинусом и синусом общего аргумента φ, т. е.
![]()
Функция у достигает своего наименьшего значения
![]()
когда sin (α + φ) = −1, и наибольшего значения
![]()
при sin (α + φ) = 1. (!)
24.15. Систему естественно привести к виду
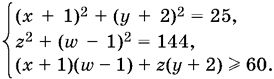
Свободные члены равны, соответственно, 5², 12² и 5 · 12. Удобно каждое из соотношений разделить на его свободный член.
Вторые указания
K главе 1
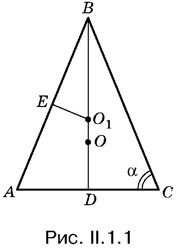
1.1. Из треугольника AO1D определить АO1; если известен радиус окружности O1 (см. рис. I.1.1 на с. 114).
1.2. Зная AB, можно найти AD и радиус ВО1 описанной окружности (рис. II.1.2). Нужно лишь заметить, что угол ABD равен /2 − α, а ВE = /2.
1.3. Возможны два случая взаимного расположения треугольника и окружности. Либо окружность будет вписана в треугольник так, что каждая точка касания делит соответствующую сторону пополам, либо одна вершина треугольника окажется внутри окружности, а две другие - вне.
Найдите решение, не зависящее от взаимного расположения окружности и треугольника. Для этого достаточно рассмотреть треугольник, который получится, если соединить середины сторон данного треугольника.
1.4. Чтобы найти отношение площадей треугольников А1В1С и АВС, нужно применить теорему об отношении площадей треугольников, имеющих равный угол.
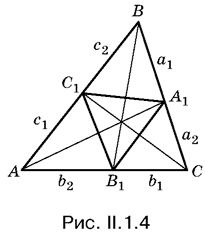
В обозначениях, введенных на рис. II.1.4. имеем
![]()
С помощью теоремы о биссектрисе внутреннего угла треугольника остается выразить а1, a2, b1, b2, c1, с2 через а, b и с.
1.5. Если центр вписанной в треугольник окружности обозначить через О, то площадь треугольника АВС можно будет вычислить как сумму площадей треугольников АОВ, ВОС и СОА. При этом каждая из сторон АО, ВО и СО может быть выражена через радиус r вписанной окружности. Площадь треугольника А1В1С1 тоже разбивается на три площади: А1ОВ1, В1ОС1 и С1ОА1. Остается углы А1ОВ1, В1ОС1 и С1ОА1 выразить через углы треугольника АВС.
1.6. Из данного соотношения между площадями треугольников АDС и АВD, имеющих общую сторону АD и одинаковые углы при вершине А (поскольку АD - биссектриса треугольника АВС), можно найти отношение сторон AC : AB. Далее применить теорему синусов.
1.7. Площадь треугольника САD (D - точка пересечения биссектрисы внешнего угла А треугольника АВС с продолжением стороны СВ) можно вычислить двумя способами, используя лишь элементы, участвующие в задаче.
1.8. Сумма двух сторон треугольника, не лежащих против угла А, участвует в выражении площади через полупериметр и радиус вписанной окружности и в выражении через биссектрису и синус половинного угла. Из этих двух выражений сумму b + с нужно исключить.
1.9. Отношение отрезков АО и ОМ дано. Эти отрезки можно рассматривать как отрезки, на которые сторона AM треугольника АВМ делится биссектрисой ВО. В результате мы перейдем к отношению отрезков AB и ВМ, последний из которых легко выражается через стороны данного треугольника.
Аналогично нужно поступить с отношением отрезков ВО и ON.
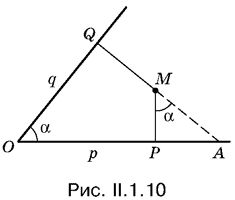
1.10. Угол РМА равен углу QОА (рис. II.1.10). Чтобы найти МР, нужно рассмотреть сначала треугольник РМА, а затем треугольник ОАQ.
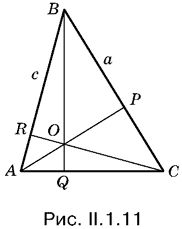
1.11. С помощью первого указания можно получить одно уравнение, связывающее углы данного треугольника. Ко второму уравнению нас приведет условие, в силу которого высота ВQ треугольника АВС (рис. II.1.11) в 6 раз больше высоты ОQ треугольника АОС. Достаточно выразить АQ из треугольников АВQ и АОQ, заметив при этом, что угол ОАQ является дополнительным для угла С.
1.12. После того как получено соотношение
/sin C + /sin B = k
использовать условие, согласно которому В − С = /2, с тем, чтобы получить уравнение относительно одной тригонометрической функции неизвестного угла С. Для достижения этой цели можно, например, в написанное выше соотношение подставить В = /2 + С. После этого полученное соотношение удобно возвести в квадрат.
1.13. Способ 1. Через x, y и z можно выразить площадь треугольника:
ха + yb + zc = 2S.
Еще три соотношения, в которых участвуют x, y и z, получим, если выразим каждый из отрезков АО, ВО и СО из двух прилегающих к нему треугольников.
Способ 2. Связать отрезки l, m и n удобно с помощью теоремы косинусов для каждого из трех треугольников АОВ, АОС и ВОС, сумма площадей которых равна площади треугольника АВС.
1.14. Остается использовать условие, что А − В = φ. С помощью формул преобразования произведения тригонометрических функций в сумму придем к тригонометрическому уравнению относительно /2.
1.15. Площадь треугольника АВС, которую мы временно обозначим через S, равна
S = ½aha = ½bhb.
Кроме того, S выражается через а, b, l и sin /2 , если треугольник АВС разделить биссектрисой СD на два треугольника.
1.16. Для нахождения угла СОВ следует использовать тот факт, что центр вписанной в треугольник окружности лежит на пересечении биссектрис. Для этого нужно выразить ∠ СОВ через сумму ∠ ОСВ + ∠ ОВС.
1.17. Так как по условию стороны треугольника образуют арифметическую прогрессию, то обозначим их длины через а, а + d, а + 2d и постараемся связать радиус вписанной окружности с длинами сторон. На рисунке треугольник удобно расположить так, чтобы средняя по длине сторона оказалась его основанием.