Конечно, второе решение выглядит более изящно, чем первое. Однако признать его лучшим трудно, поскольку за те простые уравнения, от которых мы отказались, пришлось уплатить некоторым усложнением логики.
А теперь приведем арифметическое решение этой задачи - решение, в котором удается обойтись вообще без составления уравнений.
Так как рабочие совместно выполнили 1 − /6 = /6 всей работы, причем третий сделал ⅓, то на долю первого и второго осталось /6 − ⅓ = ½ всей работы. Следовательно, если бы первый и второй успели выполнить всю работу, то третий за то же самое время сделал бы ⅔; ему останется 1 − ⅔ = ⅓ , на что ему потребовалось бы в силу последнего условия задачи 9 ч.
Так как каждый рабочий сделал одинаковое количество деталей, т. е. ⅓ всей работы, то третий работал ровно 9 ч. Тогда второй работал 9 + 2 = 11 ч. Так как он тоже сделал ⅓ всей работы, то его производительность равна /33 всей работы в час. Мы знаем, что первый и второй тратят на ½ всей работы столько же, сколько третий на ⅓, т. е. 9 ч. Второй сделает за это время 33 · 9 = /11 всей работы. Следовательно, на долю первого приходится ½ − /11 = /22. Его производительность /22 : 9 = /198 в час. Свою треть работы он выполнил за ⅓ : /198 = 13/5 (ч), т. е. за 13 ч 12 мин.
Хотя решение выглядит намного красивее, чем первые два, его тоже трудно назвать существенно лучшим. Взгляните внимательно на уравнения второго решения, и вы заметите, что третье решение получено почти "дословным" пересказом этих уравнений.
Таким образом, на пути к решению задачи вас не должно останавливать большое число неизвестных, которые, по вашему мнению, следует ввести.
Однако старайтесь не вводить неизвестные, размерность которых не встречается в условии и не может быть получена как комбинация элементов условия. Введение таких неизвестных может усложнить задачу.
Вот простой пример.
Пример 2. Расстояние между двумя пунктами A и В пароход проходит по течению реки на а ч быстрее, чем то же расстояние в стоячей воде, и на b ч быстрее, чем против течения (b > а > 0). За какое время пароход проходит расстояние от A до В по течению?
Если ввести в рассмотрение неизвестные: v - скорость парохода в стоячей воде, w - скорость течения реки, x - расстояние, то получим систему двух уравнений с тремя неизвестными:
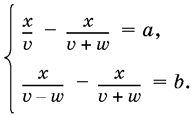
Найти из этой системы величину /v + w можно, если сделать следующие преобразования:

и обозначить /x = у, /x = z. Мы придем к системе относительно у и z, решив которую, вычислим /y + z.
Однако такую систему можно было получить сразу, если бы мы не ввели в качестве неизвестного x пройденное пароходом расстояние.
В условии задачи не было чисел, выраженных в километрах, однако расстояние между пунктами являлось существенным связующим звеном. Это означает, что мы должны были принять его за единицу, а скорости v и w выражать в частях расстояния, пройденных за один час. В результате мы пришли бы к системе

которую не пришлось бы преобразовывать.
Разберем еще одну задачу, на примере которой видно, как решаются задачи на движение.
Пример 3. Из пункта С в пункт D выехал товарный поезд. Через 5 ч 5 мин навстречу ему из пункта D выехал пассажирский поезд. Они встретились в каком-то пункте А. После этого пассажирский поезд приехал в пункт С через 4 ч 6 мин, а товарный - в пункт D через 12 ч 55 мин. Сколько времени каждый поезд находился в пути?
Условия задачи можно отразить на схеме (рис. 18.1), где буквой В обозначено положение товарного поезда в момент выхода пассажирского из пункта D.

То обстоятельство, что оба поезда находились в точке А одновременно, мы отразим на схеме с помощью вертикального отрезка, связывающего оба пути. Схема подсказывает нам и выбор неизвестных. На путь от В до А товарный поезд потратил столько же времени, сколько пассажирский на путь от пункта D до А. Если обозначить это время через x, то на схеме не останется "белых пятен".
Пусть v1 - скорость товарного поезда, а v2 - скорость пассажирского поезда. Каждый из отрезков пути: от пункта С до А и от пункта D до А позволяет составить уравнения
12/12v1 = хv2, (5/12 + x)v1 = 4/10v2.
Можно составить и уравнение для всего пути:
(5/12 + x + 12/12)v1, = (x + 4/10) v2,
которое является следствием (точнее, суммой) первых двух уравнений. Однако это уравнение проще второго. Поэтому мы будем решать систему

Разделив первое уравнение на второе, получим