Двумя часами позже я был полностью очарован. Джон с энтузиазмом описывал свои представления о том, как пространство и время становятся бешеным, дрожащим, пенящимся миром квантовых флуктуаций, когда рассматриваешь их в чудовищной силы микроскоп. Он сказал мне, что самая глубокая и вдохновляющая проблема физики - это объединение двух великих эйнштейновских теорий - общей теории относительности и квантовой механики. Он объяснил, что лишь на планковском расстоянии элементарные частицы раскрывают свою истинную природу, и она должна быть целиком геометрической - квантово-геометрической. На глазах молодого честолюбивого физика важный бизнесмен превратился в идеалистического мечтателя. Больше всего на свете я хотел последовать в бой за этим человеком.
Был ли на самом деле Джон Уилер столь консервативным, каким он казался? Честно говоря, я не знаю. Но он определенно не был ханжой-морализатором. Однажды, когда Джон и мы с женой Энни выпивали в прибрежном кафе Вальпараисо, он поднялся со словами, что хочет прогуляться и посмотреть на южноамериканских девушек в бикини. В то время ему было уже сильно за восемьдесят.
Как бы то ни было, я так никогда и не стал одним из уилеровских мальчиков; Принстон меня не принял. Так что я отправился в Корнелл, где физика была куда слабее. Прошло много лет, прежде чем я вновь ощутил тот же трепет, что в 1961 году.
Где-то около 1967 года Уилер очень заинтересовался гравитационно сколлапсировавшими объектами, которые Карл Шварцшильд описал в 1917 году. Тогда они назывались черными или темными звездами. Но это не отражало сущности данных объектов - тот факт, что это глубокие дыры в пространстве, гравитационное притяжение которых непреодолимо. Уилер стал называть их черными дырами. Сначала знаменитый американский физический журнал Physical Review отказался использовать такое название. Сегодня причина этого выглядит смешной: термин "черная дыра" считался непристойным! Однако Джон пробил его через редакционную коллегию, и черные дыры вышли в свет.
Забавно, что следующий тезис Джона гласил: "Черные дыры не имеют волос". Не знаю, возражал ли Physical Review на этот раз, но терминология закрепилась. Уилер вовсе не пытался провоцировать редакторов. Напротив, он приводил очень серьезные соображения относительно свойств горизонтов черных дыр. Под "волосами" он имел в виду наблюдаемые свойства - какие-нибудь кочки или другие неоднородности. Уилер отмечал, что горизонт черной дыры гладкий и лишен каких-либо деталей, подобно лысой голове, - на самом деле он еще намного более гладкий. Когда черная дыра образуется - скажем, при коллапсе звезды, - горизонт очень быстро приобретает форму идеальной, без каких-либо особенностей, сферы. Если не считать массы и скорости вращения, любая черная дыра совершенно неотличима от других. По крайней мере, так считалось.
Израильтянин Якоб Бекенштейн - маленький тихий человек. Но его мягкое поведение в научном сообществе контрастирует с его интеллектуальной смелостью. В 1972 году он был одним из аспирантов Уилера, заинтересовавшимся черными дырами. Однако они занимали его не как небесные тела, которые когда-нибудь можно будет увидеть в телескоп. Страстью Бекенштейна были основания физики, ее самые фундаментальные принципы, и он чувствовал, что черные дыры могут рассказать о законах природы нечто очень важное. Особенно его интересовал вопрос, терзавший и Эйнштейна: как черные дыры уживаются с принципами квантовой механики и термодинамики. По сути, стиль физических исследований Бекенштейна был очень похож на эйнштейновский; оба они были мастерами мысленного эксперимента. По минимуму используя математику, но очень глубоко размышляя о принципах физики и о том, как их применять в воображаемых (но возможных) физических условиях, оба ученых могли получать далеко идущие выводы, которые сильно влияли на будущее физики.
Вот вкратце вопрос, который поставил Бекенштейн. В вашем распоряжении контейнер с горячим газом, имеющим высокий уровень энтропии. Вы бросаете контейнер с энтропией в черную дыру. Здравый смысл говорит, что контейнер просто исчезнет под горизонтом. С точки зрения любых практических задач энтропия полностью исчезнет из наблюдаемой Вселенной. Согласно доминирующему представлению, гладкий, лысый горизонт не способен скрывать никакую информацию. Так что будет казаться, что энтропия мира убывает, что противоречит второму началу термодинамики, который говорит, что энтропия никогда не убывает. Неужели можно так легко нарушить столь важный принцип, как второе начало? Эйнштейн бы ужаснулся.
Бекенштейн заключил, что второе начало слишком глубоко встроено в систему физических законов, чтобы так легко нарушаться. Поэтому он выдвинул радикально новое предположение: сами черные дыры должны обладать энтропией. Он утверждал, что при подсчете общей энтропии Вселенной - недостающей информации в звездах, межзвездном газе, атмосферах планет и всех ваннах с горячей водой - необходимо добавить определенное количество энтропии в счет каждой черной дыры. Благодаря этой идее Бекенштейн спас второе начало. Эйнштейн, без сомнения, одобрил бы это.
Вот как рассуждал Бекенштейн. Энтропия всегда сопутствует энергии. Она связана с числом комбинаций чего-то, а это что-то во всех случаях является энергией. Даже чернила на этой странице состоят из имеющих массу атомов, которые, согласно Эйнштейну, обладают энергией, поскольку масса - это форма энергии. Можно сказать, что энтропия соответствует числу возможных способов организации порций энергии.
Когда Бекенштейн в своем воображении засовывал контейнер с горячим газом в черную дыру, он добавлял ей энергию. Это оборачивалось увеличением массы и размеров черной дыры. Вели, как предположил Бекенштейн, черные дыры имеют энтропию, которая растет вместе с их массой, то появляется шанс спасти второе начало. Энтропия черной дыры должна возрастать сильнее, чем необходимо для компенсации потерь.
Прежде чем рассказывать, как Бекенштейн вывел формулу для энтропии черной дыры, надо объяснить, почему эта идея была такой шокирующей, что, согласно Хокингу, он первоначально отбросил ее как вздорную.
Энтропия учитывает различные варианты организации, но что это такое? Если горизонт черной дыры лишен деталей, как самая гладкая из мыслимых лысин, то что там подсчитывать? По этой логике, черная дыра должна иметь нулевую энтропию. Утверждение Джона Уилера о том, что "черные дыры не имеют волос", выглядит прямо противоречащим теории Якоба Бекенштейна.
Как примирить учителя и студента? Позвольте привести поясняющий пример. Отпечаток на листе с разными градациями серого в действительности состоит из крошечных черных и белых точек. Предположим, в нашем распоряжении имеется миллион черных точек и миллион белых. Один из возможных рисунков получается, если разделить страницу пополам по вертикали или по горизонтали. Одну половину можно сделать черной, другую - белой. Есть только четыре способа выполнить это.

Получается четкий рисунок с резкими контрастами, но имеющий всего несколько вариаций. Четкий рисунок с резкими контрастами обычно означает низкую энтропию.
Теперь выберем другую крайность и равномерно распределим по той же площади равное число черных и белых пикселов. Получится более или менее однородный серый цвет. Если пикселы действительно маленькие, этот серый фон будет выглядеть совершенно однородным. Имеется колоссальное число способов перераспределить черные и белые точки так, что мы не различим варианты без увеличительного стекла.
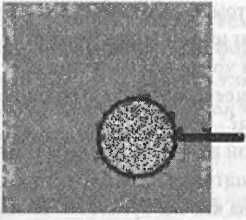
В этом случае видно, что высокая энтропия часто сопутствует однородному, "лысому" виду.
Связь внешней однородности и высокой энтропии указывает на нечто важное. Она подразумевает, что система, какой бы она ни была, должна состоять из большого числа микроскопических объектов, которые (а) слишком малы, чтобы их увидеть, и (б) могут комбинироваться множеством разных способов без изменения общего вида системы.