Как уже говорилось, инвестиционные проекты, результаты применения управляющих воздействий к процессам налогообложения и другие экономические реалии описываются финансовыми потоками (потоками платежей и поступлений), т. е. функциями (временными рядами), а сравнивать функции естественно с помощью тех или иных характеристик (критериев).
Критерии (показатели, характеристики финансовых потоков), используемые при анализе инвестиционной деятельности, можно подразделить на две группы в зависимости от того, учитывается или нет временной параметр. А именно: а) основанные на дисконтированных оценках; б) основанные на учетных (номинальных) оценках. К первой группе относятся:
– чистая текущая стоимость (Net Present Value, NPV, по-английски [нет прэзнт в э лью]) ;
– индекс рентабельности инвестиции (Profitability Index, PI, [профитэб и лити и ндэкс]);
– внутренняя норма доходности (Internal Rate of Return, IRR, [инт ё нал р э йт ов рет ё н]);
– модифицированная внутренняя норма доходности (Modified Internal Rate of Return, MIRR, [модиф а йд инт ё нал р э йт ов рет ё н]);
– дисконтированный срок окупаемости инвестиции (Discounted Payback Period, DPP, [диск а унтид пэйб э к пер и од]).
Ко второй группе относятся:
– срок окупаемости инвестиции (Payback Period, PP, [пэйб э к пер и од]);
– коэффициент эффективности инвестиции (Accounting Rate of Return, ARR, [акк а унтин р э йт ов рит ё н]).
Чистая текущая стоимость. Этот критерий основан на сопоставлении величины исходных инвестиций ( I С ) с общей суммой дисконтированных чистых денежных поступлений, генерируемых проектом в течение прогнозируемого срока. Поскольку приток денежных средств распределен во времени, он дисконтируется с помощью коэффициента q . Выбор значения этого коэффициента может осуществляться из различных соображений. Например, он может быть установлен аналитиком (выступающим от имени инвестора), исходя из ежегодного процента возврата, который инвестор хочет или может иметь на инвестируемый им капитал.
Допустим, делается прогноз, что исходные инвестиции ( IС ) будут генерировать в течение n лет годовые доходы в размере Р 1 , Р 2 , …, P n . Общая накопленная величина дисконтированных доходов (Present Value, PV) и чистая текущая стоимость (Net Present Value, NPV) соответственно рассчитываются по формулам:
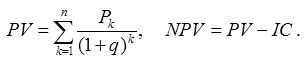
Очевидно, что если NPV > 0 , то проект целесообразно принять; если NPV < 0 , то проект целесообразно отвергнуть; при NPV = 0 проект не является ни прибыльным, ни убыточным.
Теперь дадим экономическую интерпретацию значению критерия NPV с позиции владельцев компании. Если NPV < 0 , то в случае принятия проекта стоимость компании уменьшится, т. е. владельцы компании понесут убыток. Если NPV = 0 , то в случае принятия проекта стоимость компании не изменится, т. е. благосостояние ее владельцев останется на прежнем уровне. Если NPV > 0 , то в случае принятия проекта стоимость компании, а следовательно, и благосостояние ее владельцев увеличатся.
При прогнозировании доходов по годам необходимо учитывать все виды поступлений как производственного, так и непроизводственного характера, которые могут быть ассоциированы с данным проектом. Так, если по окончании периода реализации проекта планируется поступление средств в виде ликвидационной стоимости оборудования или высвобождения части оборотных средств, они должны быть учтены как доходы соответствующих периодов.
Если проект предполагает не только разовые инвестиции, но и последовательное инвестирование финансовых ресурсов в течение т лет, то формула для расчета NPV модифицируется следующим образом:
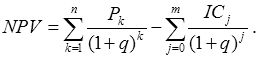
где IC 0 = IC .
Необходимо отметить, что показатель NPV отражает прогнозную оценку изменения экономического потенциала организации в случае принятия рассматриваемого проекта. Этот показатель аддитивен в пространственно-временном аспекте, т. е. NPV различных проектов можно суммировать. Это очень важное свойство, выделяющее этот критерий из всех остальных и позволяющее использовать его в качестве основного при анализе оптимальности инвестиционного портфеля.
Как уже отмечалось, не всегда инвестиции сводятся к одномоментному вложению капитала, а возврат происходит равными порциями. Чаще приходится анализировать поток платежей и поступлений общего вида. Будем в качестве потока платежей и поступлений рассматривать последовательность a(0), a(1), a(2), a(3), …, a(t), …. Если величина a(k) отрицательна, то это платеж, а если она положительна – поступление. Выше был рассмотрен важный частный случай – поток с одним платежом a(0) = ( – IC ) и дальнейшими поступлениями a (1) = Р 1 , a (2) = Р 2 , …, a ( n ) = P n .
Чистую текущую стоимость, или, как ее иногда называют, дисконтированную прибыль, чистый приведенный доход (или эффект, или величину), т. е. разность между дисконтированными доходами и расходами, рассчитывают для потока платежей путем приведения затрат и поступлений к одному моменту времени:
NPV = a(0) + a(1) С (1) + a(2) С (2) + a(3) С (3) + … + a(t)С(t) + … (4),
где С(t) – дисконт-функция, определяемая по формулам (2) или (3). В простейшем случае, когда дисконт-фактор не меняется год от года и согласно формуле (1) имеет вид С = 1/(1+q ), где q – банковский процент, формула для чистой текущей стоимости конкретизируется:
NPV = NPV ( q ) = a (0) + a (1)/(1 +q ) + a (2)/(1 +q ) 2 +
+ a (3)/(1 +q ) 3 + … + a ( t )/(1 + q ) t + ….(5)
Пример 1. Пусть a (0) = – 10, a (1) = 3, a (2) = 4, a (3) = 5. Пусть q = 0,12, тогда, как установлено выше, согласно формуле (2) значения дисконт-функции таковы: С (1) = 0,89, С (2) = 0.80, а С (3) = 0,71. Тогда согласно формуле (4)
NPV (0,12) = – 10 + 3 × 0,89 + 4 × 0.80 + 5 × 0,71 =
= – 10 + 2,67 + 3,20 + 3,55 = – 0,58.
Таким образом, этот проект является невыгодным для вложения капитала, поскольку NPV (0,12) отрицательно, в то время как при отсутствии дисконтирования (т. е. при С = 1, q = 0) вывод иной: NPV (0) = – 10 + 3 + 4 + 5 = 2 > 0, проект выгоден.
Таким образом, важной проблемой является выбор дисконт-функции. В качестве приближения обычно используют постоянное дисконтирование, хотя экономическая история последних лет показывает, что банки часто меняют проценты платы за депозит, так что формула (3) для дисконт-функции с различными процентами в разные годы более реалистична, чем формула (2).
Часто предлагают использовать норму дисконта, равную приемлемой для инвестора норме дохода на капитал. Это предложение означает, что экономисты явным образом обращаются к инвестору как к эксперту, который должен назвать им некоторое число исходя из своего опыта и интуиции. Кроме того, при этом игнорируется изменение указанной нормы во времени.
При использовании чистой текущей стоимости значение экономического эффекта во многом определяется выбранным для расчета нормативом (коэффициентом) дисконтирования – показателя, используемого для приведения по фактору времени ожидаемых денежных поступлений и платежей. Выбор численного значения этого показателя зависит от таких факторов, как:
• цели инвестирования и условия реализации проекта;
• уровень инфляции в конкретной национальной экономике;
• величина инвестиционного риска;
• альтернативные возможности вложения капитала;
• финансовые и иные соображения и представления инвестора .
Считается, что для различных классов инвестиций могут выбираться различные значения коэффициента дисконтирования. В частности, вложения, связанные с защитой рыночных позиций предприятия, оцениваются по весьма низкому нормативу 6 %. Инвестициям в обновление основных фондов соответствует норматив дисконтирования 12 %, а вложениям с целью экономии текущих затрат – 15 %. Для вложений, нацеленным на увеличение доходов предприятия, используют коэффициент дисконтирования 20 %, а для рисковых капиталовложений – 25 %. В литературе подчеркивается зависимость коэффициента дисконтирования от степени риска проекта. Для обычных проектов приемлемой считается ставка 16 %, для новых проектов на стабильном рынке – 20 %, для проектов, базирующихся на новых технологиях, – 24 %.