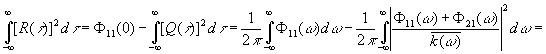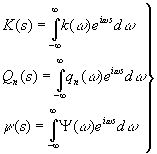
, (3.80)
то
. (3.81)
Следовательно,
. (3.82)
Этот вывод мы используем для того, чтобы получить оператор предсказания в форме, связанной не со временем, а с частотой. [c.146]
Таким образом, прошлое и настоящее функции ξ(t, γ), или точнее "дифференциала" dξ(t, γ), определяют прошлое и настоящее функции f(t, γ), и обратно.
Если теперь А >0, то
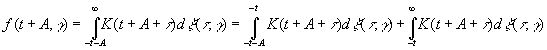(3.83)
Здесь первый член последнего выражения зависит от области изменения dξ(τ, γ), в которой, зная лишь f(σ, γ) для σ≤t, сказать ничего нельзя, и совершенно не зависит от второго члена. Его среднеквадратическое значение равно
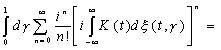, (3.84)
и эта формула дает все статистическое знание о нем. Можно показать, что первый член имеет гауссово распределение с этим среднеквадратическим значением. Последнее равно ошибке наилучшего возможного предсказания функции f(t+A, γ).
Само же наилучшее возможное предсказание выражается вторым членом в (3.83):
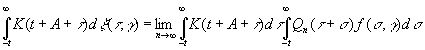. (3.85)
Если теперь положим
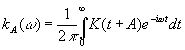(3.86)
[c.147]
и применим оператор (3.85) к e, получив
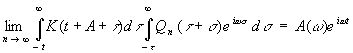, (3.87)
то найдем, подобно (3.81), что
(3.88)
Это и есть частотная форма наилучшего оператора предсказания.
Задача фильтрации в случае временных рядов типа (3.34) тесно связана с задачей предсказания. Пусть сумма сообщения и шума имеет вид
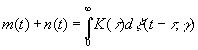, (3.89)
а сообщение имеет вид
, (3.90)
где γ и δ распределены независимо в интервале (0, 1). Тогда предсказуемая часть функции m(t+a), очевидно, равна
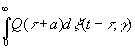, (3.901)
а среднеквадратическая ошибка предсказания равна
. (3.902)
Допустим, кроме того, что нам известны следующие величины:
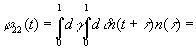[c.148]
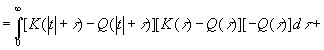
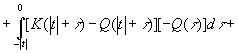
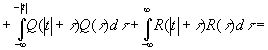
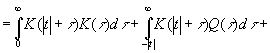
(3.903)
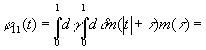
(3.904)
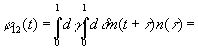
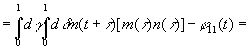
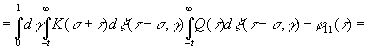
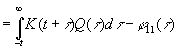(3.905)
[c.149]
Преобразование Фурье для этих величин соответственно равно
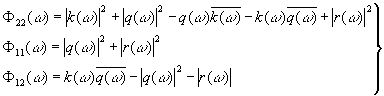(3.906)
где
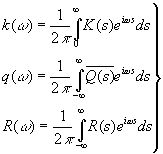
(3.907)
то есть
(3.908)
и
, (3.909)
где для симметрии пишем
.
Теперь мы можем определить k(ω) из (3.908), как прежде определили k(ω) из (3.74). Здесь мы принимаем
В результате
(3.910)
и
. (3.911)
Таким образом, наилучшее определение функции m(t) с наименьшей среднеквадратической ошибкой есть
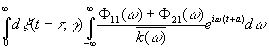. (3.912)
[c.150]
Сравнивая это с уравнением (3.89) и пользуясь рассуждениями, подобными тем, посредством которых было получено (3.88), заключаем, что оператор для m(t)+n(t), дающий "наилучшее" представление функции m(t+a), имеет при записи в частотной шкале следующий вид:
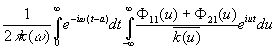. (3.913)
Этот оператор служит характеристическим оператором устройства, которое в электротехнике называют волновым фильтром. Величина а есть фазовое отставание фильтра. Она может быть положительной или отрицательной; если она отрицательна, то а называется фазовым опережением. Прибор, соответствующий формуле (3.913), может быть построен с какой угодно точностью. Подробности его конструкции нужны более для инженера-электрика, чем для читателя этой книги. Их можно найти в соответствующей литературе.
Среднеквадратическая ошибка фильтрации (3.902) может быть представлена как сумма среднеквадратической ошибки фильтрации для бесконечного фазового отставания
